Торговля и инфраструктура
Страна, обладающая ресурсами в размере 90 единиц труда, производит два товара — иксы (X) и игреки (Y). Для производства единицы икса или единицы игрека необходимы 2 единицы труда.
На мировом рынке игреки вдвое дороже иксов. Страна является малой экономикой, то есть воспринимает цены мирового рынка как заданные и не может на них влиять.
Чтобы торговать на мировом рынке, нужно уметь доставлять из страны на мировой рынок экспортируемый товар и, наоборот, доставлять с мирового рынка в страну импортируемый товар. Для этого нужна транспортная инфраструктура. Обслуживание транспортной инфраструктуры, позволяющей перевезти в любую сторону x иксов и y игреков, требует единиц труда.
Назовем множеством торговых возможностей (МТВ) множество всех наборов (x,y), которые достижимы для страны с помощью производства и торговли.
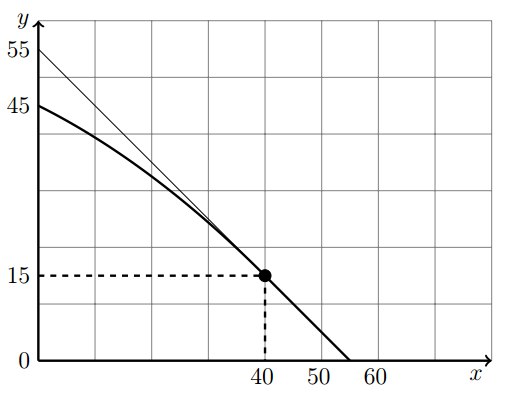
Постройте и задайте аналитически границу МТВ.
Ответ
На мировом рынке страна будет продавать игреки и покупать иксы в силу сравнительного преимущества — альтернативная стоимость одного игрека внутри страны постоянна и равна 2/2=1, в то время как на мировом рынке игреки вдвое дороже иксов. При международной торговле количество иксов и игреков, участвующих в сделке на мировом рынке, будет относиться как 2:1 (за один игрек дают два икса), так как по условию игреки вдвое дороже иксов.
Преобразуем функцию транспортных затрат, избавившись от одной из переменных. Пусть страна участвует в международной торговле и обменивает иксов на игреков. Тогда:
Пусть — располагаемое (после торговли) количество иксов, равное сумме произведённого внутри страны и купленного на рынке. Аналогично, . Тогда . Будем искать максимально возможное количество Y для всех X. Будем оптимизировать функцию , считая X параметром, на зависящей от X области определения. Область определения можно найти из рассуждения, что количество произведённых иксов не может быть отрицательным: , откуда .
Весь труд тратится на три вида деятельности: производство иксов и игреков, а так же на транспортировку.
Графиком функции является квадратичная парабола с ветвями вниз. Максимум достигается в вершине . Но вершина попадает в область определения только когда , то есть . В противном случае максимум будет на правой границе области определения .
Следовательно, один участок границы МТВ имеет следующий вид:
Другой участок границы МТВ имеет такой вид:
Запишем итоговый ответ:
