Продаются картины
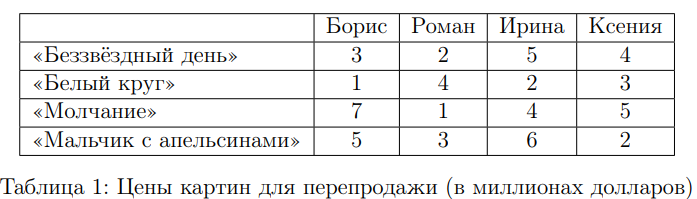
Ценители искусства Борис, Роман, Ирина и Ксения приехали на закрытую выставку произведений известного художника с целью приобрести картины, а затем перепродать их в своих странах по более высокой цене. Картин всего четыре: «Беззвёздный день», «Белый круг», «Молчание», «Мальчик с апельсинами». В разных странах полотна оцениваются по-разному. В таблице 1 указаны цены картин (в миллионах долларов), по которым каждый из ценителей искусства может перепродать их в своей стране.
Художник устанавливает цены на все четыре картины: P_1, \ P_2, \ P_3, \ P_4 — одновременно. Информация о цене каждой из картин в разных странах известна всем участникам выставки. Каждый посетитель закрытой выставки может увезти с собой лишь одну картину — таковы правила художника. Ценитель искусства максимизирует свою прибыль: разницу между ценой, за которую данную картину удастся перепродать, и ценой, назначенной за неё художником. Если ценителю искусства все равно, какую картину покупать и покупать ли её вообще, он будет приобретать ту, цена перепродажи которой выше. Если на одну картину претендуют несколько человек, художник продает её тому ценителю, в стране которого она оценивается выше.
а) ( 7 баллов) Найдите цены, которые установит художник, если он максимизирует собственный доход.
Прибыль художника складывается из цен P_1, \ P_2, \ P_3, \ P_4. Наибольшая цена, которую каждый из ценителей искусства готов заплатить за данную картину, — цена в стране, откуда этот посетитель выставки приехал. Поскольку художник может продать всего одну картину каждому ценителю, то наиболее выгодно продать ценителю ту картину, за которую он готов платить больше всего, если это возможно.
Так картина «Белый круг» будет продана Роману за 4 млн долларов, так как это самая высокая цена продажи этой картины, а также самая большая цена, которую готов платить Роман.
Ксения и Борис готовы заплатить наибольшую сумму за картину «Молчание», однако Борис готов заплатить больше, поэтому цена P_3=7 позволит художнику заработать больше, а Ксения по такой цене эту картину покупать не будет.
Тогда останутся картины «Беззвёздный день» и «Мальчик с апельсинами». Заметим, что Ирина готова за каждую из оставшихся картин заплатить больше, чем Ксения. Необходимо рассмотреть два случая. Предположим, что Ирине должна достаться картина «Мальчик с апельсинами» по цене P_4=6 (цена перепродажи в родной для Ирины стране). Если Ксении достанется «Беззвёздный день» по цене 4 млн долларов, то Ирина тоже будет претендовать на эту картину. Для того, чтобы Ирине было выгоднее купить оставшуюся картину «Мальчик с апельсинами», придётся установить на него цену равную 5 млн долларов. Теперь прибыль Ирины от перепродажи картины «Мальчик с апельсинами» будет равна 6-5=1 млн долларов, что не меньше прибыли от перепродажи других картин. Пусть теперь Ирине достанется картина «Беззвёздный день» по цене P_1=5 (максимальной для неё), а Ксении — «Мальчик с апельсинами» по цене P_4=2. Суммарная прибыль такого распределения картин уже меньше, однако художнику придётся ещё и снизить цену на картину «Беззвёздный день», чтобы Ирина не захотела её поменять.
Таким образом, художник получит прибыль в размере 20 млн долларов.
б) ( 9 баллов) Пусть художник хочет, чтобы первая картина досталась Борису, вторая — Роману, третья — Ирине, четвёртая — Ксении. Может ли он установить такие цены, что четверо ценителей искусства сами выберут картины таким способом?
Мы знаем, что художник устанавливает цены P_1, \ P_2, \ P_3, \ P_4. Для того, чтобы Борису было выгоднее купить первую картину, должны выполняться следующие неравенства
\begin{cases} 3 - P_1 \ge 1 - P_2, \\ 3 - P_1 > 7 - P_3, \\ 3 - P_1 > 5 - P_4. \end{cases}
Здесь 3-P_1 — прибыль Бориса от продажи первой картины, 1-P_2 — от продажи второй картины и т.д. Заметим, что если Андрей получает картину, за которую готов заплатить больше всего, то с Борисом и, например, с Ириной дела обстоят иначе. Ирина получает ту картину, за которую Борис готов заплатить больше, а Борис получает ту картину, за которую больше готова платить Ирина. Вероятно, этот факт приведёт нас к противоречию, запишем систему уравнений для Ирины.
\begin{cases} 4 - P_3 \ge 5 - P_1, \\ 4 - P_3 \ge 2 - P_2, \\ 4 - P_3 > 6 - P_4. \end{cases}
Рассматривая системы уравнений для Ирины и для Бориса, выберем те, которые соответствуют нежеланию Бориса выбрать третью картину и нежеланию Ирины выбрать первую картину
\begin{cases} 3 - P_1 \ge 7 - P_3, \\ 4 - P_3 \ge 5 - P_1. \end{cases}
Из этих двух уравнений получим, что P_3-P_1>4, а также -1>P_3-P_1, что невозможно. Получается, нельзя подобрать такие цены, чтобы картины были распределены таким образом.
Комментарий. Полученное противоречие не является единственным. Участник может рассматривать любые системы уравнений и их комбинации. В таком случае, при условии отсутствия ошибок в решении, за этот пункт так же выставляется полный балл.
в) ( 9 баллов) Художник решил, что картина «Мальчик с апельсинами» должна достаться Ксении. Найдите все возможные комбинации цен, которые он может установить, чтобы это выполнялось, или покажите, что таких цен не существует.
Для того, чтобы Ксении не хотела купить картину «Мальчик с апельсинами», должны выполняться следующие неравенства
\begin{cases} 2 - P_4 > 4 - P_1, \\ 2 - P_4 > 3 - P_2, \\ 2 - P_4 > 5 - P_3 \end{cases} \Rightarrow \begin{cases} P_1 - P_4 > 2, \\ P_2 - P_4 > 1, \\ P_3 - P_4 > 3. \end{cases}
Рассмотрим Ирину. Для того, чтобы Ирина не хотела купить четвертую картину, должно выполняться хотя бы одно из следующих неравенств
\begin{cases} 5 - P_1 > 6 - P_4, \\ 2 - P_2 > 6 - P_4, \\ 4 - P_3 > 6 - P_4 \end{cases} \Rightarrow \begin{cases} P_1 - P_4 < -1, \\ P_2 - P_4 < -4, \\ P_3 - P_4 < -2. \end{cases}
Заметим, что это противоречит системе уравнений, записанной для Ксении.
Комментарий. Полученное противоречие не является единственным. Участник может рассматривать любые системы уравнений и их комбинации. В таком случае, при условии отсутствия ошибок в решении, за этот пункт так же выставляется полный балл.
Это значит, что не существует набора цен, при котором она сама выбрала бы четвёртую картину, однако стоит помнить, что существует принцип, по которому, в случае нескольких претендентов на одну и ту же картину, художник определяет нового владельца. Получается, что даже если Ксения захочет купить другую картину, она может ей не достаться, если есть конкурент. Покажем, как художник может воспользоваться этим фактом.
На картину «Мальчик с апельсинами» нельзя установить цену больше двух, иначе Ксения её не приобретёт. В таком случае, все остальные ценители не будут претендовать на эту картину при следующем условии:
\begin{cases} 7 - P_3 > 5 - P_4, \\ 7 - P_2 > 3 - P_4, \\ 5 - P_1 > 6 - P_4 \end{cases} \Rightarrow \begin{cases} P_3 \le 2 + P_4, \\ P_2 \le 1 + P_4, \\ P_1 \le -1 + P_4. \end{cases}
Следует отметить, что такое распределение картин наиболее полно описывает возможные комбинации цен, поскольку оставшиеся картины достаются тем, кто их может перепродать дороже. Получается, что для каждого значения цены 1<P_4\leq 2 существует набор цен P_1, \ P_2, \ P_3, описываемый системой выше.