Немного про Джини
В фирме «Равенство и Братство» есть только две группы работников: менеджеры и аналитики. Внутри группы каждому работнику выплачивается одинаковая заработная плата, причём зарплата аналитиков более низкая. Коэффициент Джини, характеризующий неравенство оплаты труда, в фирме «Равенство и Братство» равен 0,3. В конкурирующей фирме «Рога и Копыта» структура персонала и оплаты труда аналогична, однако коэффициент Джини равен 0,5. (Примечание: коэффициент Джини измерен в долях, то есть максимальное значение коэффициента Джини по используемой шкале равно 1). Фонд оплаты труда в обеих фирмах одинаковый и составляет 1 млн. руб. Известно, что зарплата менеджеров фирмы «Рога и Копыта» в 1,5 раза выше зарплаты менеджеров фирмы «Равенство и Братство». При этом доля аналитиков в обеих фирмах совпадает. Какова доля аналитиков в общем количестве персонала в фирмах?
Условие про 1 млн. руб. лишнее.
В случае, когда есть две однородные группы, кривая Лоренца выглядит так:
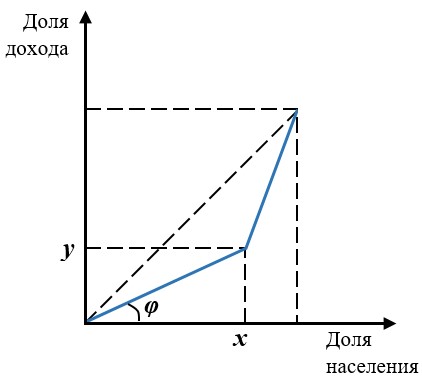
Сначала поясним, как найти индекс Джини, зная долю доходов бедных и долю их численности.
Площадь под кривой Лоренца равна:
\frac{1}{2} xy + y + \frac{1}{2} (1 - x) = \frac{1}{2} (y - x + 1)
Площадь между кривой равномерного распределения доходов и кривой Лоренца:
\frac{1}{2} - \frac{1}{2} (y - x + 1) = \frac{1}{2} (x - y)
Таким образом, индекс Джини равен: G = \frac{1}{2} (x - y) = \frac{1}{2} (x - y)
G=x−y, где x – доля бедных (в этом случае доля аналитиков), а y – это доля фонда оплаты труда, приходящаяся на аналитиков (4 балла за соотношение). Фирму «Равенство и Братство» обозначим индексом 1, а «Рога и Копыта» – индексом 2. Можем записать следующие уравнения:
\begin{aligned} y_1 &= 1 - 1,5y_1 = 1 - 0,5, \\ y_2 &= 1 - 1,5y_1 = 1,5y_1 - 0,5 \end{aligned} \quad (3 \text{ балла})
Также известно, что G_1 = x - y_1, G_2 = x - y_2
Решая, получаем, что x = 3G_1 - 2G_2 + 1 = 3 \cdot 0,3 - 2 \cdot 0,3 - 0,5 = 0,9
Ответ:
0,9