Задание 4. Олимпиада Колокольникова 2024 (7 класс)
Покорение Сибири
В двух сибирских городах, Тюмени и Тобольске, торгуют изделиями из кости мамонта. Спрос на изделия в Тюмени задается уравнением Q_1^d=100-3P, предложение Q_1^s=2P. В Тобольске спрос задан функцией Q_2^d=80-P, а предложение Q_2^s=4P-40. Торговля между городами отсутствует.
а) ( 5 баллов) Найдите цены на изделия в обоих городах.
Найдем первоначальные цены, приравняв спрос и предложение в городах.
( 1 балл за упоминание и/или использование равенства спроса и предложения)
Q_1^d = Q_1^s \Rightarrow 100 - 3P_1 = 2P_1 \Rightarrow P_1 = \frac{100}{5} = 20. ( 2 балла)
Q_2^d = Q_2^s \Rightarrow 80 - P_1 = 4P_1 - 40 \Rightarrow P_1 = \frac{120}{5} = 24. ( 2 балла)
б) ( 6 баллов) Между городами проложили торговый путь. Какой теперь будет цена на изделия?
В Сибирь приплыл Ермак и решил налаживать экономику региона. Для этого он ввел потолок цен на торговлю между городами на уровне P=16.
Теперь между городами есть торговля, следовательно, нужно сложить спросы и предложения. Заметим, что в Тюмени неотрицательный спрос при ценах ниже в 100/3, Тобольске при ценах ниже 80, а также наименьшие цены, при которых производители будут продавать изделия в двух городах, соответственно равны 0 и 40/4=10.
Следовательно, общий спрос будет равен
Q_d = Q_1^d + Q_2^d = 100 - 3P + 80 - P = 180 - 4P ( 2 балла, 1 из которых за ограничения) при P<\frac {100}{3},
а общее предложение равно
Q_s = Q_1^s + Q_2^s = 2P + 4P - 40 = 6P - 40 ( 2 балла, 1 из которых за ограничения) при P\geq 10.
Приравняем спрос и предложение:
180 - 4P = 6P - 40 \quad \Rightarrow \quad 10P = 220 \quad \Rightarrow \quad P = 22 ( 2 балла), а значит, условие 10\leq P< \frac{100}{3} удовлетворяется.
в) ( 4 балла) Найдите новое равновесие в каждом городе.
Ермак установил цену на торговлю на уровне ниже, чем изначальные равновесные, значит, торговля не выгодна продавцам обоих городов и торговли между городами не будет. Тогда получаем равновесия как в первом пункте. ( 2 балла за обоснование)
Тюмень - P_1=20, \ Q_1=2*20=40 ( 1 балл)
Тобольск - P_2=24, \ Q_2=4*24-40=56 ( 1 балл)
г) ( 5 баллов) Как и на сколько изменилось общественное благосостояние в регионе после прихода Ермака?
Для справки. Величина общественного благосостояния (SW) равна сумме излишка потребителей (CS) и излишка производителей (PS).
Посчитаем общественное благосостояние в условиях торговли и при ее отсутствии.
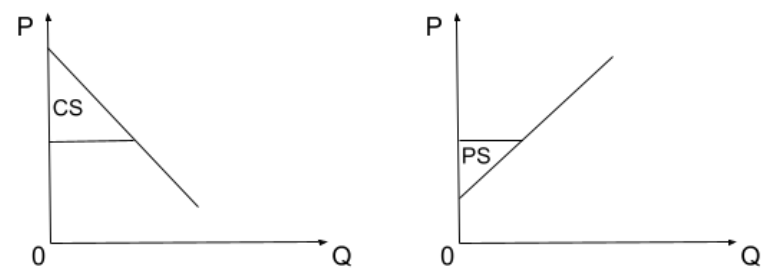
CS = \frac{(P_{\max} - P)Q}{2}; \quad PS = \frac{(P - P_{\min})Q}{2}.
Сначала посчитаем общественное благосостояние в условиях торговли:
CS_1 = \frac{\left(\frac{100}{3} - 22\right) \times 34}{2} = \frac{578}{3};
PS_1 = \frac{22 \times 44}{2} = 484;
CS_2 = \frac{58^2}{2} = 1682;
PS_2 = \frac{12 \times 48}{2} = 288.
Тогда SW = CS_1 + PS_1 + CS_2 + PS_2 = \frac{578}{3} + 484 + 1682 + 288 = 2646\frac{2}{3}.
( 2 балла, но если лишь часть излишков посчитана верно, то ставится 1 балл)
Теперь посчитаем общественное благосостояние после прекращения торговли:
CS_1^* = \left(\frac{100}{3} - 20\right) \times 40 = \frac{800}{3};
PS_1^* = \frac{20 \times 40}{2} = 400;
CS_2^* = \frac{56^2}{2} = 1568;
PS_2^* = \frac{14 \times 56}{2} = 392.
Тогда SW^* = CS_1^* + PS_1^* + CS_2^* + PS_2^* = \frac{800}{3} + 400 + 1568 + 392 = 2626\frac{2}{3}. ( 2 балла, но если лишь часть излишков посчитана верно, то ставится 1 балл)
Значит, искомое \Delta SW = SW^* - SW = 2626\frac{2}{3} - 2646\frac{2}{3} = -20, то есть общественное благосостояние уменьшится на 20 ( 1 балл)