Большая красная кнопка
Набегавшись за прошедшие два тайма, футболист Петя решил утолить жажду. В автомате рядом с футбольной площадкой продаются два его любимых напитка – сок и кола. Можно заказывать любое число (не обязательно целое) стаканов сока и колы по цене 1 рубль за стакан любого напитка. Покупая колу, можно нажать на большую красную кнопку: тогда стакан колы будет стоить всего 0,5 рубля, но при этом необходимо заказать не менее 4 стаканов колы.
В распоряжении Пети 5 рублей, которые он вовсе не обязательно целиком потратит на сок и колу: это зависит от его предпочтений в отношении сока, колы и всех остальных благ. Однако в одном мы можем быть уверены: если выбранный Петей набор из определенного количества сока и колы может быть получен разными способами (нажимая или не нажимая на большую красную кнопку), то Петя предпочтёт тот способ, который требует меньшую сумму денег.
Откладывая по оси X стаканы сока, а по оси Y – стаканы колы, изобразите на рисунке множество всех возможных наборов (x,y), которые сможет потребить Петя. Существует ли среди этих наборов такой, что, выбирая его, Петя не станет нажимать на большую красную кнопку? Если да, то покажите на рисунке множество всех таких наборов.
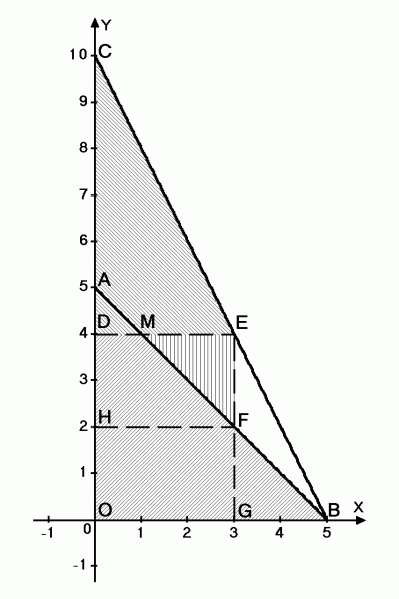
Т.к. на свои 5 рублей Петя может купить любое количество стаканов сока и колы по 1 рублю за стакан, то ему доступны любые наборы (x,y), удовлетворяющие неравенству 1 \cdot x + 1 \cdot y \leq 5, т.е. ему доступны все точки \Delta OAB.
Если он покупает не менее 4 стаканов колы, то он может нажать на кнопку, и его ограничение будет иметь вид 1 \cdot x + 0,5 \cdot y \leq 5. Таким образом, все точки \Delta DCE также являются доступными.
Однако объединением этих двух треугольников множество доступных наборов не ограничивается. Рассмотрим \Delta MEF. Любая его точка может быть получена переносом некоторой точки \Delta DCE вниз параллельно оси Y. Иными словами, Петя нажимает на кнопку и покупает большое количество колы, но выпивает её не всю, а лишь столько, сколько соответствует данной точке внутри \Delta MEF. Таким образом, все точки \Delta MEF являются доступными.
В то же время никакие манипуляции не сделают доступными точки \Delta EFB (конечно, кроме точек, лежащих на стороне EF ): ведь при количестве сока, большем 3 стаканов, Пете бессмысленно нажимать на кнопку, т.к. на 4 стакана колы денег ему уже не хватит.
Итак, множеством доступных наборов является пятиугольник OCEFB.
Теперь найдём доступные наборы, выбирая которые, Петя не станет нажимать на кнопку. Очевидно, что в каждом из них y < 4. В предыдущем параграфе мы убедились, что при x > 3 Петя не будет нажимать на кнопку, так что смело включаем в искомое множество \Delta GFB (часть множества доступных наборов, в которой x > 3 и y < 4 ), пока что без стороны FG. В отличие от \Delta GFB, \Delta MEF не войдёт в искомое множество, т.к. точки MEF достигаются лишь при нажатии кнопки.
Но даже из оставшейся части множества доступных наборов -- фигуры ODMFG, -- мы исключим некоторую область, которая не войдёт в искомое множество. Этой областью является трапеция HDMF. Несмотря на то, что в ней y \leq 4, Петя сможет потребить то же количество колы, заплатив меньше денег, если нажмёт на кнопку и закажет ровно 4 стакана колы по цене 0,5 рубля за стакан: он выпьет свои y стаканов, но при этом сэкономит (1 \times y - 4 \times 0,5) рублей. Итак, если Петя захочет потребить набор из трапеции HDMF, то он обязательно нажмёт на кнопку (за исключением разве что стороны HF, где ему безразлично, нажимать кнопку или нет).
А вот прямоугольник OHFG мы включим в искомое множество: если Петя здесь нажмёт на красную кнопку, то сэкономить уже не сможет (он не сможет понизить цену в два раза, обойдясь при этом менее чем двукратным увеличением количества стаканов).
Итак, Петя обойдётся без нажатия кнопки, если выбранный им набор принадлежит трапеции OHFB.