Pandemic Possibility Frontier
Last year, IEO contestants were asked to solve a problem about an optimal lockdown. Unfortunately, in 2021 this topic is no less relevant. So suppose society is facing a severe viral pandemic and contemplates introducing a lockdown. How strong should the lockdown be? The answer to this question apparently depends on the preferences of the society between the lives/health of people and GDP. Or does it really?
Let d \in [0, 1] be the level (strength) of a lockdown (d=0 is no lockdown while d=1 is complete lockdown) and \nu be some measure of the total amount of virus in circulation. The relation between the two is given by \nu = 2(1 − d). Aggregate demand in the economy is given by the function Y = 10 − 2d − P while aggregate supply is governed by the equation Y = 2 + P − d − \alpha \cdot \nu where \alpha \geq 0 is a parameter; Y is real GDP and P is price level, as usual. Finally, let H be the aggregate health of people; it depends on the amount of virus in circulation as follows: H = 3 − \nu /2.
Define the Pandemic Possibility Frontier (PPF, for short) as the set of all pairs (Y, H) that can be achieved by a policy-maker by choosing various levels of lockdown d \in [0, 1].
(a) (7 rp) Give a reason for why \alpha may be positive.
A positive \alpha means that the amount of virus has a direct negative effect on aggregate supply. This may be due to an adverse effect of the virus on labor supply: people who are sick or have died cannot work. Also, when the amount of virus grows, some people may choose voluntarily to work from home rather than from office and, at least in some occupations, this lowers labor productivity and thus GDP supplied.
(b) (16 rp) Sketch the PPF and show the coordinates of its extreme points if \alpha=1 and \alpha=2 (on two different diagrams).
It is convenient to derive the PPF equation for all \alpha at once. First, equate aggregate demand and aggregate supply:
10 - 2d - P = 2 + P - d - \alpha v,
so equilibrium price level is P = \frac{8 - d + \alpha v}{2} = 4 - \frac{d}{2} + \frac{\alpha v}{2}, and thus, equilibrium GDP is Y = 2 + P - d - \alpha v = 6 - \frac{3d}{2} - \alpha v/2. Plugging v = 2(1 - d) in the last equation, we get
Y = 6 - \frac{3d}{2} - \alpha (1 - d) = 6 - \alpha - \left( \frac{3}{2} - \alpha \right) d.
Health, in its turn, depends on the level lockdown as follows:
H = 3 - \sqrt{v}/2 = 3 - (1 - d) = 2 + d.
Note that since d \in [0,1] H ranges from 2 to 3.
To derive the PPF, we eliminate d from the last two equations by expressing it, say, in terms of H and plugging the result into the equation for Y. Namely, d = H − 2, so finally
Y = 6 - \alpha - \left( \frac{3}{2} - \alpha \right)d = 6 - \alpha - \left( \frac{3}{2} - \alpha \right)(H - 2) = 9 - 3\alpha - \left( \frac{3}{2} - \alpha \right)H.
Now it is easy to answer parts (b) and (c).
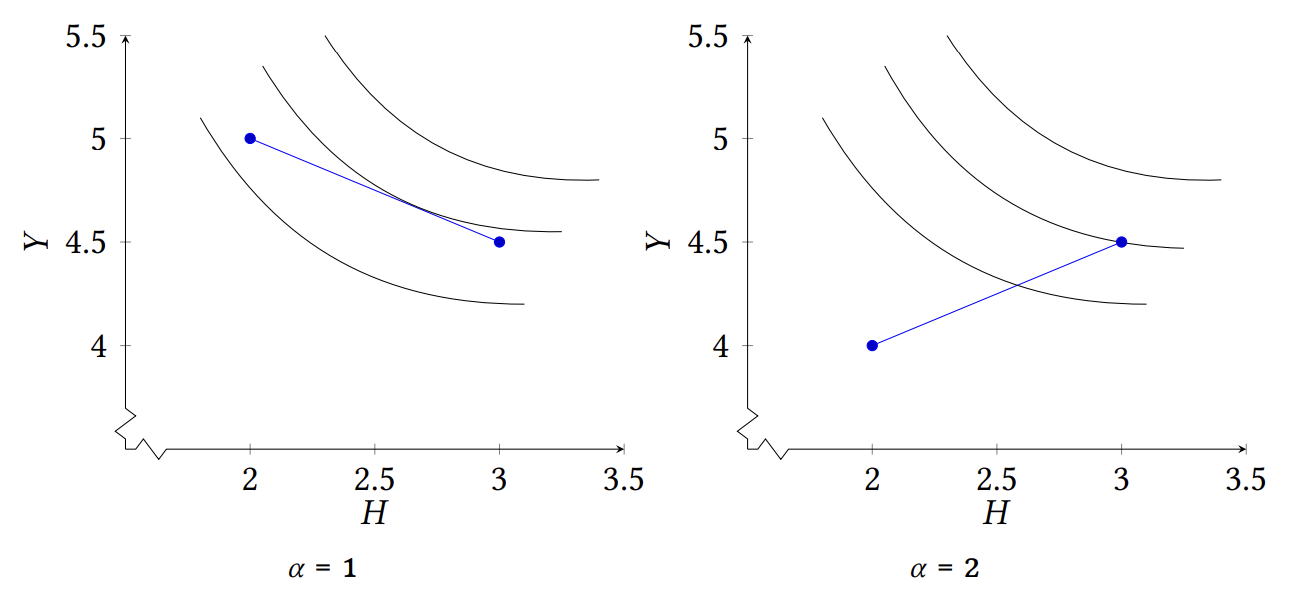
For \alpha=1 the PPF equation is Y = 6 − H /2. It is a downward-sloping line with extreme points (2, 5) and (3, 4.5) (recall that H takes values from 2 to 3). The first point corresponds to d=0 and the second to d=1.
For \alpha=2 the PPF equation is Y = 3 +H /2. It is a upward-sloping line with extreme points (2, 4) and (3, 4.5). The first point corresponds to d=0 and the second to d=1.
(c) (7 rp) Suppose the preferences of the society over GDP-Health combinations (Y,H) are given by some family of indifference curves. In practice, no one knows a society's indifference curves exactly; this generates heated debate about the optimal level of lockdown. For which values of \alpha a policy-maker does not have to know the society's indifference curves over(Y,H) in order to find the optimal level of lockdown? (The policy-maker still knows all the data in the task and assumes correctly that the society values each of Y and H.)
If the PPF is downward-sloping, the optimal lockdown depends nontrivially on the society's preferences as different families of indifference curves will give rise to different points of tangency with the PPF. There is a nontrivial trade-off between lives and GDP that can be resolved only with the knowledge of society's preferences.
On the other hand, if the PPF is upward-sloping (or flat), the society should choose the rightmost point on the PPF regardless of its preferences since this point generates the highest possible levels of GDP and Health simultaneously. There's no trade-off. Thus, the optimal lockdown will be unambiguously d^*=1; one won't have to know the society's preferences in order to make this conclusion.
So it remains to find for which \alpha the PPF is upward-sloping or flat. From our general derivation above, we see that this will happen if and only if \alpha \geq 3/2.
Note that our conclusion is intuitive: a strong lockdown becomes good for both Health and GDP and there is no trade-off exactly when the negative effect of the virus on labor supply is strong enough.
Comment. Modern economic modeling and statistical techniques allow to estimate a Pandemic Possibility Frontier on real data. For example, economists Greg Kaplan, Benjamin Moll and Giovanni L. Violante have estimated (https://www.nber.org/papers/w27794) the Pandemic Possibility Frontier for the US in the context of COVID-19 pandemic. The PPF turns out to be downward-sloping and highly nonlinear. The authors estimated the effect of various non-lockdown policies on the location and shape of the frontier. Beside that, the authors coined the very term Pandemic Possibility Frontier for which we credit them.