Как в одной большой стране завод строили
Президент одной очень большой страны недавно решил, что пора заняться импортозамещением. Беда в том, что в стране до этого ничего не производилось, поэтому необходимой инфраструктуры в ней тоже не было. В связи с этим президент приказал своей команде обеспечить строительство завода, который бы позволял производить высокий рейтинг (обозначим как X) и стабильность (обозначим как Y).
Команда, которой было поручено столь ответственное дело, решила провести тендер. Его выиграла пара иностранных специалистов Mr.Vasilich и Mr.Petrovich. Они сказали, что завод будет характеризоваться двумя параметрами, а именно размером телевизора (в метрах квадратных, обозначим как A), который будет подбадривать рабочих завода, и весом летающего медведя (в кг, обозначим как B), который будет парить по заводу и заставлять рабочих работать. КПВ завода зависит от этих параметров и описывается следующим образом:
Василич способен производить либо 8 кв. метров телевизора, либо 2 кг веса медведя, либо любую их линейную комбинацию. Петрович же способен производить либо 2 кв. метра телевизора, либо 8 кг веса медведя, либо любую их линейную комбинацию. Когда специалисты обратились к заказчику с вопросом, какие параметры нужно выбрать, тот впал в ступор, потому что он забыл спросить у президента, в каком количестве высокий рейтинг и стабильность нужно производить, а снова идти к президенту ему не хотелось. Немного подумав, он решил, что оптимальными будут такие a и b, при которых множество доступных пар (x;y), то есть площадь под КПВ, будет максимально, после чего делегировал нахождение этих параметров вам.
Найдите оптимальные a и b.
Найдем общее КПВ специалистов:
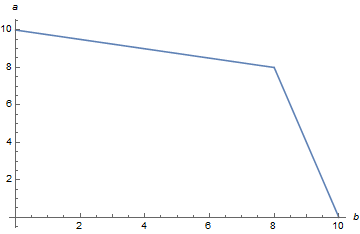
Теперь преобразуем КПВ завода:
Это уравнение окружности с центром в (−10+a;−10+b) и радиусом a. Рассмотрим это графически:
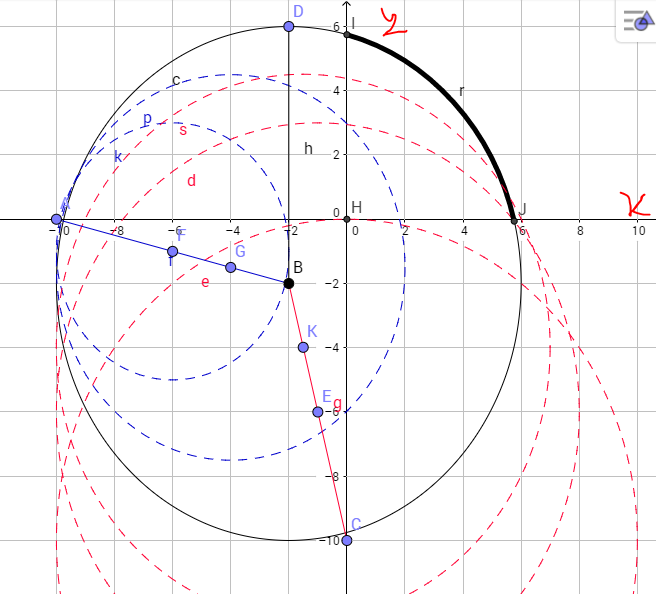
(Строго говоря, там должны быть не окружности, а полуокружности без левой части. Однако на первую четверть графика это никак не влияет, а именно она нас и интересует)
Центр окружности может лежать либо на ломаной ABC, либо левее и ниже неё. Очевидно, что площадь будет больше, если центр будет лежать где-то на прямой. Поместим его в точку (−10;0) и поедем вправо. Очевидно, что до точки B площадь будет расти, после этой точки - падать. Значит максимальная площадь достигается при центре окружности в точке (−2;−2) при a=b=8
Ответ:
a=8
b=8