Из пункта Н в пункт С
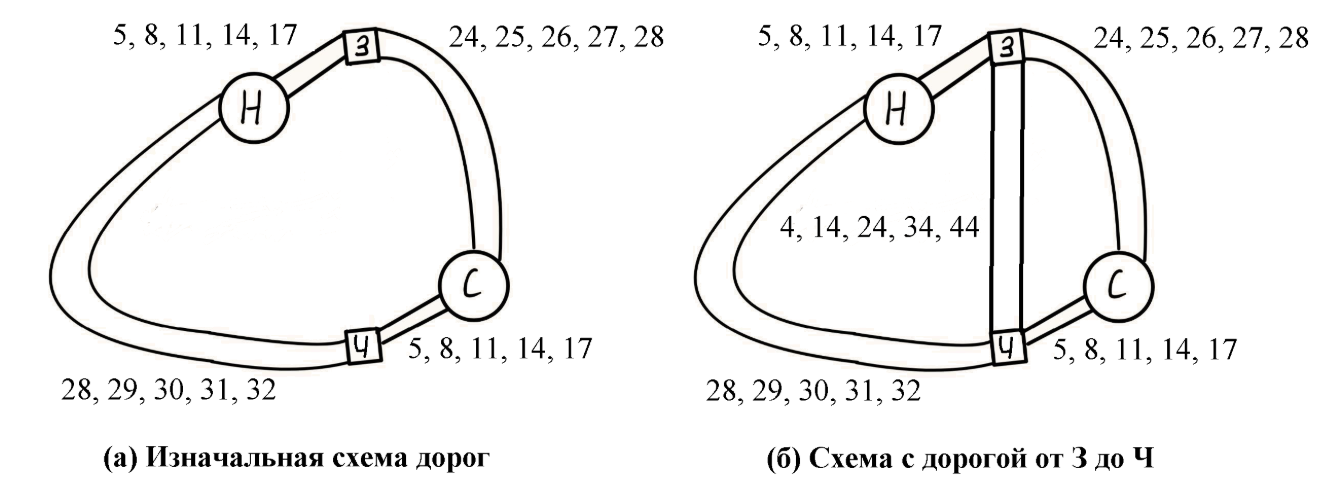
Наступает конец недели и 5 автомобилистов направляются к себе на дачи. Все они едут из города Новобимск (обозначен буквой Н на схеме под буквой (а)) в город Старобимск (С). Каждому автомобилисту доступны два пути через относительно небольшие города Забимск (З) и Чернобимск (Ч).
Новобимск и Забимск соединены короткой проселочной однополосной дорогой. Одному автомобилю потребуется 5 минут, чтобы проехать соответствующий участок дороги, а каждый дополнительный автомобиль, проезжающий в то же время, увеличит время в пути на 3 минуты. Чернобимск и Старобимск соединены аналогичной дорогой.
Старобимск и Забимск соединяет скоростное двухполосное шоссе. Одному автомобилю потребуется 24 минуты на его преодоление, а каждый дополнительный автомобиль увеличит время в пути на 1 минуту. Новобимск и Чернобимск соединены несколько более длинным шоссе, так что время в пути от одного города до другого для одного автомобиля составит 28 минут, а каждый дополнительный автомобиль увеличит время в пути на 1 минуту. Все автомобилисты выбирают маршрут и отправляются в путь одновременно, а также хотят как можно быстрее добраться до своей дачи. Если автомобилисты едут по одной и той же дороге, то их скорость одинакова.
а) Назовем равновесием ситуацию, при которой ни один автомобилист не захочет поменять свой маршрут, зная, какие маршруты выбрали другие автомобилисты. Найдите все равновесия и докажите, что других равновесий нет. Сколько времени в пути потратит каждый автомобилист в найденных вами равновесиях?
Предположим, что между Забимском и Чернобимском построили новую скоростную двухполосную трассу. Движение на этой трассе одностороннее: пользуясь этой трассой, можно добраться из Забимска в Чернобимск, но не наоборот. Новая схема дорог указан под буквой (б) на Рисунке. Автомобилистам теперь доступны несколько маршрутов от Н до С (в обозначениях, введенных ранее): через Забимск (для удобства обозначим такой путь Н-З-С), через Забимск и Чернобимск (Н-З-Ч-С), а также через Чернобимск (Н-Ч-С). Для того, чтобы проехать дорогу от З до Ч одному автомобилю потребуется 4 минуты, а каждый дополнительный автомобиль увеличит время в пути на 10 минут. Если другой автомобиль появляется на участке (любой) дороги после того, как автомобилист начал движение по этому участку, но до того, как водитель закончил движение по участку, то время движения увеличится так же, как если бы автомобили выехали на участок трассы одновременно.
Для удобства оформления в дальнейших пунктах обозначим число автомобилистов, которые едут по маршрутам Н-З-С, Н-Ч-С и Н-З-Ч-С как x, \ y, \ z соответственно.
В равновесии некоторое количество автомобилей едут по пути Н-Ч-С, а остальные автомобили — по пути Н-З-С. Запишем в таблицу возможные варианты. Первая и третья колонки таблицы будут означать число автомобилистов на Н-Ч-С и Н-З-С соответственно. Вторая и четвёртая колонки — время в пути.
\begin{array}{|c|l|c|l|} \hline y & \text{Время Н-Ч-С} & x & \text{Время Н-З-С} \\ \hline 0 & \text{---} & 5 & 28 + 17 = 45 \\ \hline 1 & 28 + 5 = 33 & 4 & 27 + 14 = 41 \\ \hline 2 & 29 + 8 = 37 & 3 & 26 + 11 = 37 \\ \hline 3 & 30 + 11 = 41 & 2 & 25 + 8 = 33 \\ \hline 4 & 31 + 14 = 45 & 1 & 24 + 5 = 29 \\ \hline 5 & 32 + 17 = 49 & 0 & \text{---} \\ \hline \end{array}
Предположим, что в равновесии y=5. Тогда конкретному автомобилисту выгодно отклониться и выбрать Н-З-С, поскольку он потратит меньше времени (29<49) ). Значит, такая ситуация не может быть равновесной. Аналогично, y\neq 4 и y\neq 3, ведь 33<45 и 37<41.
Предположим теперь, что x=5. Тогда конкретному автомобилисту выгодно отклониться и выбрать Н-Ч-С, поскольку он потратит меньше времени (33<45). Значит, такая ситуация не может быть равновесной. Аналогично, x\neq 4, поскольку 37<41.
Таким образом, единственное потенциальное равновесие соответствует случаю, при котором x=3, \ y=2.
Тогда автомобилистам на Н-Ч-С не выгодно отклоняться (41>37), равно как и автомобилистам на Н-З-С (41>37).
Среднее время в пути, как и время каждого конкретного автомобилиста, составит 37 минут.
б) Приведите пример равновесия в новой ситуации и покажите, что это действительно равновесие.
Решение пункта (б) следует из пункта (в), поэтому мы решим пункт (в). Участник Конкурса мог решить пункт (б). Если пункт (в) решён полностью, то за пункт (б) также выставляется максимальный балл.
в) Единственно ли равновесие, найденное вами в предыдущем пункте? Найдите все равновесия или покажите, что других не существует.
Рассмотрим все возможные ситуации.
Пусть z=0. Тогда, исходя из пункта (а), в равновесии x=3, \ y=2. Однако, если автомобилист, избравший путь Н-З-С, отклонится и поедет по пути Н-З-Ч-С, его время в пути составит 11+4+5=20<37 минут. Значит, в равновесии z\neq0.
Рассмотрим теперь z\geq 3. Тогда время в пути на Н-З-Ч-С составляет не менее 11+24+11=46 минут. Если вместо этого поехать по пути Н-З-С, время не превысит 17+26=43 минуты. Значит, равновесное значение z может быть равно только 1 или 2.
Для оставшихся значений z составим таблицы, аналогичные пункту (а).
Сперва рассмотрим z=1 :
\begin{array}{|c|l|c|l|c|l|} \hline y & \text{Время Н-Ч-С} & x & \text{Время Н-З-С} & z & \text{Время Н-З-Ч-С} \\ \hline 0 & \text{---} & 4 & 27 + 17 = 44 & 1 & 17 + 4 + 5 = 26 \\ \hline 1 & 28 + 5 = 33 & 3 & 26 + 14 = 40 & 1 & 14 + 4 + 5 = 23 \\ \hline 2 & 29 + 8 = 37 & 2 & 25 + 11 = 36 & 1 & 11 + 4 + 5 = 20 \\ \hline 3 & 30 + 11 = 41 & 1 & 24 + 8 = 32 & 1 & 8 + 4 + 5 = 17 \\ \hline 4 & 31 + 14 = 45 & 0 & \text{---} & 1 & 5 + 4 + 5 = 14 \\ \hline \end{array}
Заметим, что время в пути по Н-З-Ч-С всегда не более 26 минут. Таким образом, автомобилисты на Н-З-Ч-С и Н-Ч-С не влияют друг на друга.
Аналогично рассуждениям из пункта (а), x\neq 4, ведь 33<44.
Также x\neq 3, так как 37<40, \ y\neq 4, потому что 32<45, и y\neq 3, ведь 36<41.
Единственное потенциальное равновесие — это ситуация, при которой x=y=2.
В этом случае никто из автомобилистов не хочет менять свой путь — ни с Н-З-С, ни с Н-Ч -С, ни с Н-З-Ч-С.
Осталось проверить отклонения в пользу Н-З-Ч-С. Для этого воспользуемся таблицей при z=2.
Теперь рассмотрим z=2 :
\begin{array}{|c|l|c|l|c|l|} \hline y & \text{Время Н-Ч-С} & x & \text{Время Н-З-С} & z & \text{Время Н-З-Ч-С} \\ \hline 0 & \text{---} & 3 & 26 + 17 = 43 & 2 & 17 + 14 + 8 = 39 \\ \hline 1 & 28 + 11 = 39 & 2 & 25 + 14 = 39 & 2 & 14 + 14 + 11 = 39 \\ \hline 2 & 29 + 14 = 43 & 1 & 24 + 11 = 35 & 2 & 11 + 14 + 14 = 39 \\ \hline 3 & 30 + 8 = 38 & 0 & \text{---} & 2 & 8 + 14 + 8 = 30 \\ \hline \end{array}
При y=1, на участке Ч-С — 11 минут, при y=2 — 14 минут. Однако при y=2, автомобилисты из Н-З-Ч-С добираются до С за 30 минут, в то время как Н-Ч-С автомобилисты только до Ч — значит, для обеих групп время на Ч-С составляет 8 минут.
x=3 не может быть равновесием, ведь 42<43. Также y\neq 3 и y\neq 2 — 35<38, \ 39<43.
Осталось y=1, \ x=z=2, но это не равновесие, т.к. автомобилисту на Н-З-Ч-С выгодно сменить путь и потратить 37 минут (см. случай z=1 ).
г) Сравните время в пути у каждого автомобилиста в отдельности и среднее время в пути у всех автомобилистов до строительства дороги, то есть в пункте (а), и после, то есть в равновесии(-ях), найденном(-ых) в пунктах (б) и (в). Объясните наблюдаемое различие. Выгодно ли строительство дороги каждому из автомобилистов? А автомобилистам в целом (исходя из среднего времени, потраченного автомобилистом в дороге)? Почему?
В новом равновесии два автомобилиста тратят в пути 37 минут, два — по 36 минут, и один — 20 минут. Ранее каждый тратил по 37 минут. Среднее время снизилось, никому не стало хуже. Это Парето-улучшение — ситуация, при которой кому-то стало лучше, а никому — хуже. Строительство новой дороги оказалось выгодным, так как сократило общее время.
д) Московский скоростной диаметр (МСД) — внутригородская скоростная магистраль, длина которой — 68 километров. МСД соединяет другие крупные автомагистрали, связывает многие районы Москвы и области. Ежедневно МСД пользуются тысячи автомобилистов. C 15 февраля 2025 года правила проезда по МСД изменились. Проезд по МСД, ранее бывший бесплатным, стал платным для всех автомобилей по будним в часы пик. Объясните, почему правительство Москвы сделало проезд по МСД платным. Приведите два аргумента.
Среди возможных аргументов:
Строительство новых дорог может стимулировать покупку автомобилей и увеличить пробки.
Снижение числа автомобилей улучшает экологическую обстановку. Выхлопные газы — пример негативного внешнего эффекта, то есть ситуации, при которой поведение одних людей ухудшает положение других.