Два касания
Фирма "В два касания" является монополистическим конкурентом на рынке волейбольных мячей. В последнее время владельцу фирмы Н. Е.Удачнику можно только посочувствовать: его бизнес переживает не лучшие времена (Кризис!). Спрос на продукцию фирмы линеен, однако в последнее время он стал настолько низким, что фирме неважно, уходить с рынка или производить 40 единиц продукции, - и это при наиболее продуманном, рациональном поведении! Средние переменные издержки при данном объеме выпуска аж втрое больше предельных, а единственным для фирмы шансом покрыть выручкой постоянные издержки было бы установление цены, равной 20.
Представьте, что вы являетесь сотрудником государственной службы, оказывающей поддержку малому бизнесу.
- Проанализируйте ситуацию, в которой оказалась фирма "В два касания", графически, изобразив на одном рисунке примерные графики спроса, MR, MC, AVC, AFC.
- Определите уравнение кривой спроса на продукцию фирмы.
- Определите величину аккордной субсидии, необходимой для выведения фирмы Н. Е. Удачника на уровень безубыточности.
В оптимуме фирме неважно, производить 40 единиц продукции или
уходить с рынка, значит,
MR(40) = MC(40)
\pi (40) = \pi (0) = -FC
\Downarrow
P(40) = AVC(40)
Более того, раз фирма не может получить прибыль большую, чем -FC , то в других точках функция AVC не будет касаться графика спроса, кроме как в точке, где Q=40.
Из условия следует, что существует лишь единственная цена (а значит, и единственный объем выпуска), при которых выручка равна постоянным издержкам. Как легко понять из графиков выручки и постоянных издержек, такая ситуация возможна, только если при этом объеме выпуска выручка максимальна. Значит, в остальных точках выручка меньше, чем постоянные издержки, а средняя выручка (цена) - меньше, чем средние постоянные издержки. Отсюда следует, что график спроса должен касаться графика AFC в точке, где P=20 и MR=0.
Пусть обратная функция спроса задается уравнением P=a-bQ . Тогда
3 = \frac{AVC(40)}{MC(40)} = \frac{P(40)}{MR(40)} = \frac{a - b \cdot 40}{a - 2b \cdot 40} \Rightarrow a = 100b.
Как мы выяснили, максимальную выручку фирма может получить при P=20. Для нашей функции спроса цена, максимизирующая выручку, равна a/2, и значит, a=40. Функция спроса, таким образом, имеет вид P=40-0,4Q.
Понятно, что величина аккордной субсидии, выводящей фирму на уровень безубыточности, должна быть в точности равна текущим убыткам фирмы (ведь после получения аккордной субсидии фирма не изменит выпуск). Значит, S = - \pi(40) = FC = TR_{\text{max}} = 20 \cdot \frac{100}{2} = 1000.
Графически ситуация сводится к следующему:
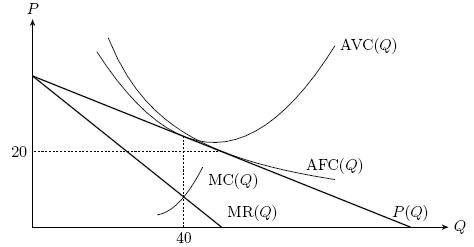
Вот такие "Два касания"!
Ответ:
- см. график.
- P=40-0,4Q.
- S=1000.