Trade Sanctions and Segmentation
There are 100 countries in the World. Demand in country number i for natural gas is given by D_i(p_i) = 100i - p_i, while its supply is given by S_i (p_i) = ip_i.
(a) (5 rp) Find equilibrium prices p_i ^* when countries do not trade with each other
(a) Equilibrium in each country can be calculated in a standard way: D_i=S_i, that is 100i − p_i = ip_i and
p_i^* = \frac{100i}{1 + i}
(b) (5 rp) Assume there is a global market for natural gas, in which all countries participate. Find the equilibrium in this market. Determine what countries are net exporters of the natural gas and what countries are net importers.
In the global market, the total demand must equal the total supply under the unified price p, so,
\sum_{i=1}^{100} (100i - p) = \sum_{i=1}^{100} (ip)
By using \sum_{i=1}^n i = \frac{n(n+1)}{2} , we get:
100 \cdot \frac{100 \cdot 101}{2} - 100p = \frac{100 \cdot 101}{2} \cdot p
Solving for p, we get:
p^*_{(b)} = \frac{100 \cdot 101}{103} \approx 98{,}06
The countries with p_i^* < p^*_{(b)} will export (they will prefer to sell to the world market).
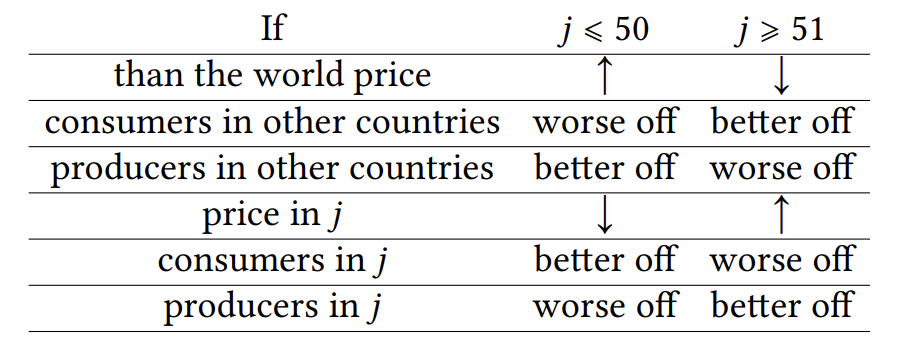
(c) (5 rp) Assume that the world imposes sanctions against country number j and discontinues trade with it. How will this affect the world price? Which agents in other countries will gain and which will lose? What can one say about the change in consumer and producer welfare in country j ?
Country j will disappear from the world market, both supply and demand. Whether it sill shift the world price up or down, depends on whether j was an exporter or importer. If it was an exporter, than under the equilibrium price, more supply will be subtracted from the world S function than demand from the world D function. Thus there will be excess demand, the price in the world will go up. If j was an importer than the world price will go down following similar logic.
This result can also be obtained analytically by subtracting demand and supply of country j and comparing the new equilibrium price with the old one.
100 \cdot \frac{100 \cdot 101}{2} - 100p - (100j - p) = \frac{100 \cdot 101}{2} \cdot p - ip
100 \cdot \frac{100 \cdot 101}{2} - 100j - 99p = \left( \frac{100 \cdot 101}{2} - i \right) \cdot p
p^*_{(c)} = \frac{505{,}000 - 100j}{5149 - j}
p^*_{(c)} > p^*_{(b)} \iff j < 50{,}5
(d) (15 rp) Now assume that the global market splits into several blocs (some perhaps consisting of a single country); there is free trade within each bloc but no trade across blocs. Answer the following questions and explain your answers, comparing the results of destruction of the global market to the free trade situation in part (b).
(d1) (5 rp) Can there be a country where the joint welfare of all consumers and all producers improve?
(d2) (5 rp) Can there be a bloc where the joint welfare of all consumers and all producers improve?
(d3) (5 rp) What happens to the joint welfare of all consumers and all producers in the world?
(d1) Yes, it is possible. To construct an example, think of a country which used to be an exporter in the global trade and remains an exporter within a block where equilibrium price is higher than p^* _{(b)}. This country is unambiguously better off. E.g., in a block with countries i = 1, 99, 100, country 1 will be the only exporter, and the price will be higher than in the equilibrium without blocs.
(d2) No. Assume such a bloc exists. If the price within this bloc is equal to p^* _{(b)}, than every agent gets the same welfare. But if it is different, this bloc (all countries in it taken together) used to be a net exporter or a net importer when the free trade was possible. No this bloc is a closed economy, so total welfare of the block must decrease when there is no across-bloc trade.
(d3) Most likely, it will go down, because there will be mutually beneficial transactions between blocs. In a particular case when in all blocs equilibrium prices turn out to be equal to p^* _{(b)}, the welfare will be the same (for example, if country 1 trades only with country 100, country 2 trades only with country 99, etc.).