Дайте концерт
Музыкальная группа «Дайте задач(!)» собирается устроить концерт. Считайте, что группа не несет никаких затрат и всегда максимизирует суммарную выручку от продажи билетов. Известно, что продажа билетов начинается за 100 дней до концерта (t=0) и заканчивается в день проведения концерта (t=100).
Фанат готов купить билет и пойти на концерт, если цена билета не превышает его готовность платить за билет, которая определяется функцией v_i(t), где t — день, в который человек i купил билет, v_i(t)=a_i+b_i*t, a_i>0, \ b_i>0. Каждый фанат приобретает билет в тот день, когда разница между его готовностью платить и ценой билета наибольшая.
Продавец устанавливает цену P_0 в первый день продаж, то есть в t=0, а затем в любой из оставшихся дней может её единожды поднять до P_1(P_1\geq P_0). Покупатели знают схему ценообразования до начала продаж, в том числе цены и день поднятия цены. Группа может продать неограниченное количество билетов, но один человек может купить только один билет. Перепродажа запрещена, если не сказано обратное. Считайте, что если человеку всё равно, в какой день купить билет, он купит в день, ближайший к концерту.
а) ( 2 балла) Приведите экономическую интерпретацию параметров a_i и b_i.
.
Коэффициент a_i определяет автономную полезность от посещения концерта. Через этот коэффициент может определяться любовь потребителя к группе. Коэффициент b_i означает прирост полезности по мере приближения ко дню концерта. Коэффициент может означать прирост полезности от прироста уверенности в том, что человек сможет пойти на концерт.
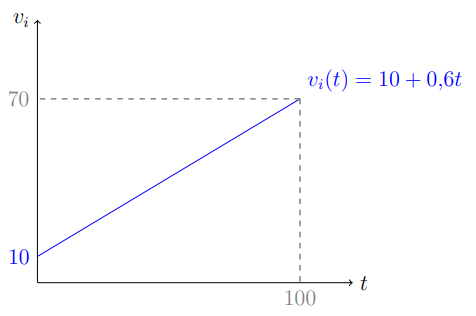
б) ( 4 балла) Найдите цены P_0 и P_1, если у всех фанатов одинаковая готовность платить равная v(t)=10+0,6t.
Продавец будет пытаться установить максимально возможную цену для группы фанатов. Заметим, что готовность платить возрастает по мере приближения к концерту. Значит, в самый последний день покупатели будут готовы заплатить наибольшую цену. Максимизирующий выручку продавец, будет продавать билет по наибольшей возможной цене, т.е. по цене в день t=100. Значит, P_1=10+100*0,6=70.
Определим, чему может быть равна цена P_0. Предположим, что он повышает цену в день \hat t. Цена P_0 должна быть такой, чтобы покупатели купили билет в последний день, т.е. она должна быть выше готовности платить в каждый из дней до \hat t : P_0\geq v_i(\hat t)=10+0,6\hat t.
в) ( 6 баллов) На рынок зашла вторая группа фанатов, равная по численности первой. Её готовность платить равна v_2(t)=a+0,1*t. Найдите цены P_0 и P_1, если a=35.
График готовностей платить имеет следующий вид:
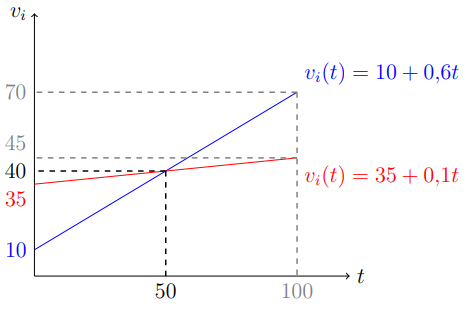
Точка пересечения находится приравниваем функций 10+0,6*t=35+0,1*t=>t=50, \ v(50)=40.
Мы видим, что до 50 дня готовность платить для группы 2 выше, чем для группы 1, а после 50 -го дня наоборот. Продавец может установить цены P_0 и P_1 таким образом, чтобы группы 2 купила по цене P_0, а группа 1 – по цене P_1. Действительно: при установлении цену P_0=40 и P_1=70 и повышении в день \hat t=51, группа 1 купит в день, предшествующий повышению (t=50), так как после него её готовность платить всегда ниже P_1=70. В то же время, группа 2 купит билет в последний день, так как во все дни, когда билеты продаются по цене P=40(t<51), её готовность платить ниже.
Проверим, что продажа, при которой мы разделяем две группы, принесёт больше прибыли, чем при установлении общей для всех цены. Будет считать, что в каждой группе N покупателей. Тогда раздельная продажа принесёт 40N+70N. Если продавец продает билет только первой группе по её максимальной цене, то прибыль, очевидно, будет меньше —70N. Если продаёт обеим группам по максимальной цене второй (100*0,1+35=45), то он получит прибыль 2*45*N (меньше, чем 110N ).
г) ( 8 баллов) Найдите цены P_0 и P_1, если a больше 10 и меньше 130. Ваш ответ должен зависеть от параметра a.
Здесь может быть рассмотрено несколько случаев, в зависимости от взаимного расположения графиков.
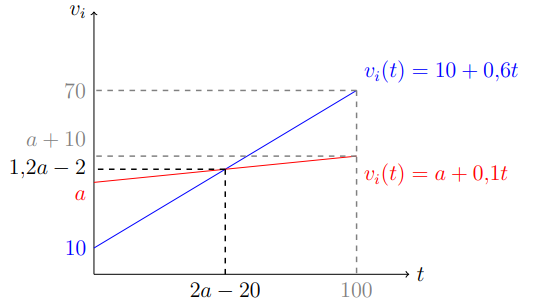
(1) Графики пересекаются в t<100. Находим пересечение: 10+0,6t=a+0,1t=>t=2a-20, v=10+0,6(2a-20)=1,2a-2. Так как t<100, \ a<60. Допустим, цены P_0 и P_1 разделяющие, как в п. в). Тогда мы продаём второй группе по P_0=1,2a-2, а первой по цене P_1=70 (аналогично пункту в) ). Прибыль в случае продажи по разным ценам: N(1,2a-2)+70N. При ограничении a<60, максимальная цена для второй группы ниже, чем для первой. Тогда, если устанавливается общая цена, то она будет равна P_1=a+10. Билеты продаются обеим группам, и выручка составит 2N(a+10). Сравниванием выручки в случае продажи по разным ценам и по одной: N(1,2a-2)+70N>2N(a+10) при ограничении a<60. После упрощения остаётся: a<60. Значит, продажа по разным ценам всегда выгоднее, чем продажа по одной цене. Таким образом, при a<60 будут установлены цены P_0=1,2a-2 и P_1=70, а повышение произойдёт в день t=2a-19.
(2) Графики не пересекаются при t<100. Такое расположение графиков будет при a\geq 60. Заметим, что при таком ограничении готовность платить второй группы будет всегда выше, чем готовность платить первой группы. Тогда продавец не сможет разделить покупателей. Тогда существует два варианта: продать в последний день только первой группе по цене P_1=a+10 или продать обеим группам по цене P_1=70. Сравниваем выручки в двух случаях: N(a+10)<70*2*N при ограничении 60\leq a<130. Упрощая неравенство, получаем a<130. Получается, при заданных ограничениях выгодно продавать обеим группам. Будет установлено P_1=70.
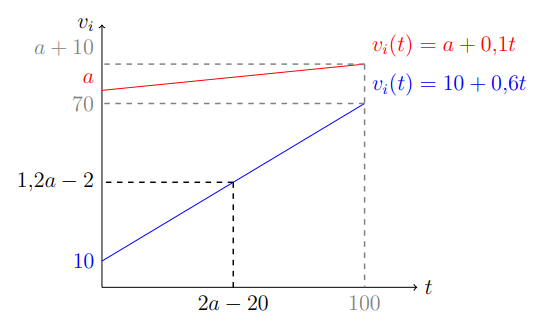
Найдём ограничения для P_0. Рассмотрим день, в который полезность второй группы достигнет 70 : a+0,1t=70, t=700-10a для 60\leq a<70. До этого дня ограничение на цену: P_0>a+0,1t, t\leq 700-10a. Если a\geq 70, то P_0>10+0,6\hat t, где \hat t — день, в который меняется цена.
д) ( 5 баллов) На рынок вошла ещё одна группа покупателей, равная по численности первой. Представители этой группы могут купить билеты в любой день и перепродать позже по более высокой цене покупателям из первой и второй группы. Выигрыш перекупщиков определяется разностью цены проданного и купленного билета. Перекупщики работают только при положительной прибыли. Считайте, что все агенты обладают полной информацией о том, как действуют все другие агенты на данном рынке. Какие цены будут установлены продавцом? Ваш ответ должен зависеть от параметра a, который больше 10 и меньше 130.
Что изменилось с появлением перекупщиков? Приведите один способ, как максимизирующий прибыль продавец может ограничить перекупщикам возможность перепродажи билетов. (Если вы приведёте более одного способа, то оцениваться будет только первый.)
В случае (2), продавец будет всегда ставить постоянную цену P_0=P_1 и перекупщики не выйдут на рынок.
Рассмотрим случай (1). Если перекупщики купят билет по цене P_0, то смогут продать его по цене P_{1} - \varepsilon и переманить всех покупателей. Тогда продавец билетов сможет поставить цену P_{1} - 2\varepsilon и т.д. Таким образом они будут конкурировать, пока не установится цена P_0. Перекупщикам невыгодно ставить такую цену и ниже, поэтому они уйдут с рынка.
Следует рассматривать 3 случая:
I. Устанавливается цена P_0=1,2a-2 для обеих групп.
II. С первого дня устанавливается цена P_1=70, покупает только первая группа.
III. С первого дня устанавливается цена P_1^{'}=a+10, покупает 2 группы.
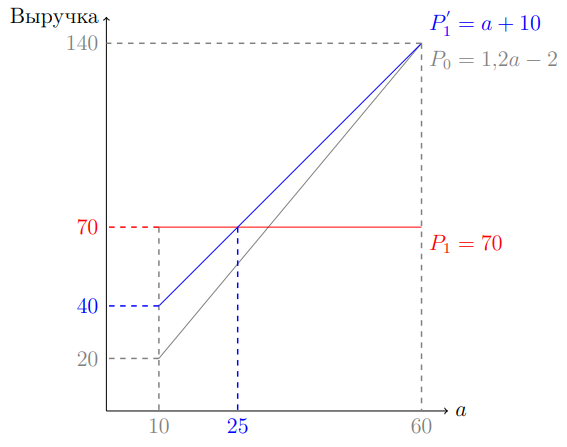
Для случаев I. и III. количество покупателей в два раза больше. Заметим, что в случае I. прибыль не выше, чем в случаях II. и III. Если a<25, то выгоднее поставить P+70. Если a>25, то выгоднее поставить P_1^{'}=a+10. Если a=25, то выручка при этих двух ценах одинаковая. С появлением перекупщиков возможность дискриминировать пропала. Для борьбы с ними можно продавать именные билеты.