Торговля и инфраструктура
Страна, обладающая ресурсами в размере 100 единиц труда, производит два товара — иксы (X) и игреки (Y). Для производства единицы икса или единицы игрека необходимы 2 единицы труда.
На мировом рынке игреки вдвое дороже иксов. Страна является малой экономикой, то есть воспринимает цены мирового рынка как заданные и не может на них влиять.
Чтобы торговать на мировом рынке, нужно уметь доставлять из страны на мировой рынок экспортируемый товар и, наоборот, доставлять с мирового рынка в страну импортируемый товар. Для этого нужна транспортная инфраструктура. Создание и обслуживание транспортной инфраструктуры, позволяющей перевезти в любую сторону x иксов и y игреков, требует L(x,y)=10+0.2x+0.6y единиц труда, (x,y) \neq (0,0). Если не участвовать в международной торговле, то можно задействовать все 100 единиц труда в производстве, никак не вкладываясь в развитие инфраструктуры и в транспортировку: L(0,0)=0. Назовем множеством торговых возможностей (МТВ) множество всех наборов (x,y), которые достижимы для страны с помощью производства и торговли.
Для выхода на мировой рынок существуют квазипостоянные издержки в виде 10 единиц труда на строительство транспортной инфраструктуры, поэтому стране может быть выгодно как участие в международной торговле, так и неучастие. Найдём все доступные комбинации двух товаров в случае выхода и невыхода на мировой рынок и объединим два этих множества.
Если страна не участвует в международной торговле, то кривая производственных возможностей выглядит следующим образом (x — количество иксов, y — количество игреков, L_i — количество труда, затраченного на производство i-го товара):
L_x = 2x,
L_y = 2y,
L = 100 2x + 2y = 100 y = 50 - x
Если страна участвует в международной торговле, то каждая единица икса или игрека может быть получена двумя способами — непосредственно произведена внутри страны с помощью труда или приобретена на мировом рынке; в последнем случае надо произвести необходимое количество другого товара, доставить его на рынок, обменять на нужный товар, затем привезти этот товар обратно в страну.
При международной торговле количество иксов и игреков, участвующих в сделке на мировом рынке, будет относиться как 2:1 (за один игрек дают два икса), так как по условию игреки вдвое дороже иксов.
Запишем выраженные в труде издержки производства иксов и игреков.
Если иксы производятся внутри страны, то необходимое для производства x иксов количество труда по условию составит Lx=2x. Если иксы покупаются на рынке, то необходимое для покупки x иксов количество труда составит L_x=2y+0,2x+0,6y=2 \cdot 0,5x+0,2x+0,6 \cdot 0,5x=1,5x. Отсюда следует, что страна не будет производить иксы, все иксы будут импортироваться.
Можно убедиться, что игреки будут производиться внутри страны: необходимое для производства y игреков количество труда по условию составит L_y=2y, в то время как если бы игреки покупались на рынке, то необходимое для покупки y игреков количество труда составило бы L_y=2x+0,2x+0,6y=2 \cdot 2y+0,2 \cdot 2y+0,6y=5y. Отсюда, в свою очередь, следует, что страна не будет импортировать игреки, все игреки будут производиться внутри. Также это следует из того, что альтернативные издержки производства игреков внутри страны составляют один икс, а цена игрека на мировом рынке — два икса.
Таким образом, если страна принимает участие в международной торговле, то кривая торговых возможностей задаётся следующим уравнением:
L_x = 1{,}5x, \ L_y = 2y, \ L = 100 - 10 = 90
1{,}5x + 2y = 90
y = 45 - 0{,}75x
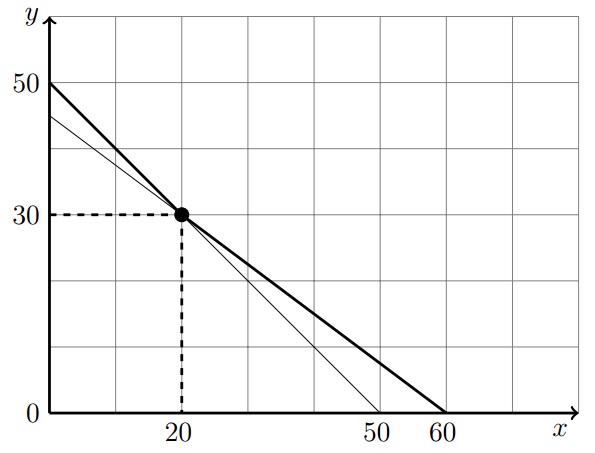
Страна будет участником международной торговли, если 45−0,75x>50−x, то есть 0,25x>5, x>20. Соответственно, при x<20 страна не будет участвовать в торговле. Поэтому множество торговых возможностей страны ограничивается ломаной линией:
y = \begin{cases} 50 - x, & 0 \leq x < 20; \\ 45 - 0{,}75x, & 20 \leq x \leq 60. \end{cases}