Задание 12. МЭ ВСоШ 2024 (7-8 класс)
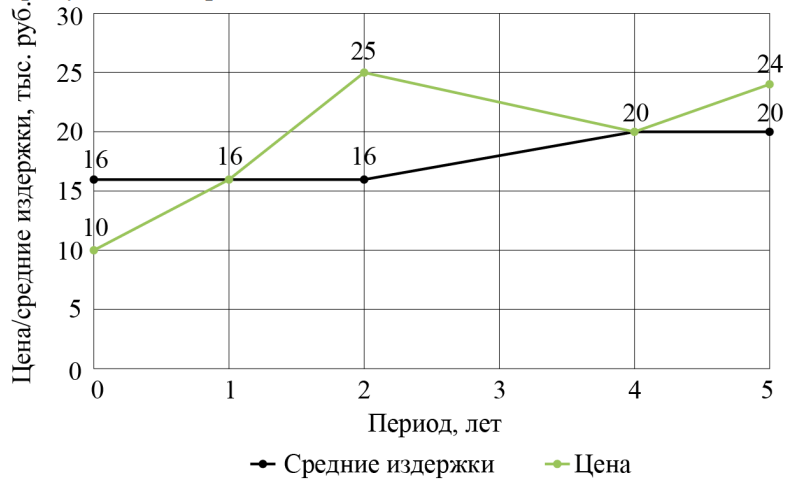
На графике ниже изображено соотношение цены и средних издержек производства продукта P в течение последних пяти лет. В рамках каждого отдельно взятого года динамика обоих показателей являлась линейной, иными словами, на любом промежутке времени внутри года темп изменения показателей оставался неизменным.
Например, в начале первого года цена была равна 10, в конце равна 16, в течение года она линейно росла от 10 до 16, тогда в середине года она была равна 13. В свою очередь, средние издержки в начале первого года были равны 16 и оставались равными 16 на протяжении всего года.
Определите, чему равна среднегодовая прибыль в тыс. рублей от продажи единицы продукта P на протяжении данных пяти лет.
Ответ: 2,5.
Решение: для ответа на вопрос необходимо просуммировать все значения разности между ценой и средними издержками и поделить результат на количество лет. Из графика понимаем, что такой сумме соответствует площадь между графиками функций, причём на участках, где цена превышает средние издержки, она берётся с плюсом, а на участках, где средние издержки превышают цену, – с минусом.
Разобьём искомую площадь на фигуры и найдём площадь каждой из них:
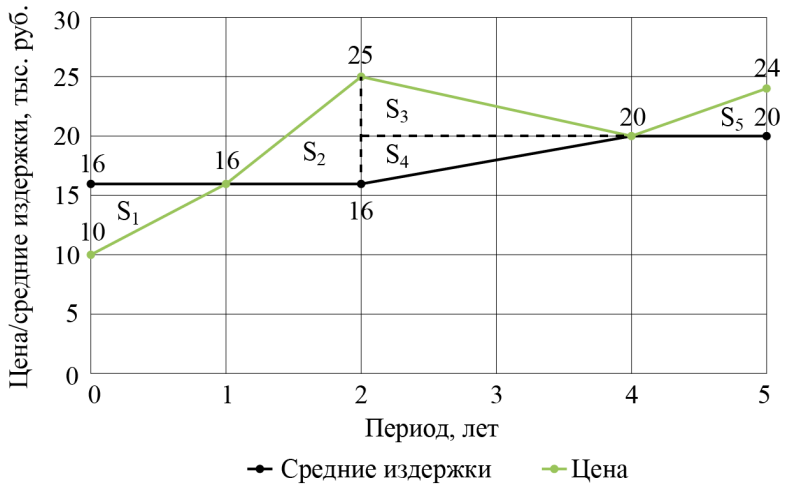
S_1 = 0{,}5 \cdot 1 \cdot (-6) = -3 \\ S_2 = 0{,}5 \cdot 1 \cdot 9 = 4{,}5 \\ S_3 = 0{,}5 \cdot 2 \cdot 5 = 5 \\ S_4 = 0{,}5 \cdot 2 \cdot 4 = 4 \\ S_5 = 0{,}5 \cdot 1 \cdot 4 = 2
Итого сумма всех площадей составит 12,5 тыс. руб., тогда среднегодовая прибыль с продукта P составит 2,5 тыс. руб.
Второй способ: определим среднюю цену и среднюю величину средних издержек:
\bar{P} = \frac{10 + 16}{2} + \frac{25 + 16}{2} + 2 \cdot \frac{25 + 20}{2} + \frac{24 + 20}{2} = \frac{13 + 20{,}5 + 25 + 20 + 22}{5} = 20{,}1 \\\bar {AC }= \frac{16 + 16 + 2 \cdot \frac{20 + 16}{2}}{5} + 20 = \frac{88}{5} = 17{,}6
Разница между ними составляет 2,5 тыс. руб., что и является ответом задачи.
За верный ответ – 8 баллов.