Послания в бутылках
Бермудский треугольник не участвует в мировой торговле, однако местные экономисты очень любят поглядывать на обстановку в других странах и получают информацию о мире из сообщений в бутылках. Так, эксперты узнали, что два острова, Антигуа и Барбуда, занимаются производством только двух товаров: сахара и кукурузы — и активно торгуют друг с другом.
а) ( 5 баллов) Известно, что кривая торговых возможностей (КТВ) Барбуды имеет линейный вид, а также устроена следующим образом: в условиях торговли остров может потребить 15 единиц сахара и не более 96 початков кукурузы, а при потреблении всего двух початков, количество сахара может возрасти до 250 единиц. Помогите экономистам Бермудского треугольника восстановить уравнение КТВ.
По условию заданы две точки: (15;96) и (250;2), а также известно, что КТВ имеет линейный вид. В таком случае, составим систему
\begin{cases} 96a + b = 15, \\ 2a + b = 250 \end{cases} \Rightarrow -94a = 235 \Rightarrow a = -2{,}5 ;
2 \cdot (-2{,}5) + b = 250 \Rightarrow b = 255.
Итоговое уравнение КТВ имеет вид Q_s=255-2,5Q_c, где Q_s и Q_c — это количество сахара и кукурузы, соответственно.
б) ( 10 баллов) В новом сообщении эксперты узнали, что кривые производственных возможностей (КПВ) обоих островов также имеют линейный вид. Кроме того, Антигуа может произвести не более 100 початков кукурузы. Какое максимальное количество кукурузы может произвести Барбуда? Ответ обоснуйте.
Зная уравнение КТВ Барбуды, найдем максимальное количество сахара и кукурузы, которое страна может произвести,
Q_{s_{\max}} = 255 - 2 \cdot 0 = 255,,
0 = 255 - 2{,}5Q_{c_{\max}} \Rightarrow Q_{c_{\max}} = 102..
Известно, что максимальное значение в потреблении определенного товара на КТВ может достигаться в трёх случаях. Первый случай, когда страна обладает сравнительным преимуществом в его производстве, максимальное количество товара, которое она может потребить при торговле (максимальное значение на КTВ) совпадает с максимальным количеством, которое она может потребить без торговли (максимальное значение на КПВ). А второй, когда страна покупает весь товар за рубежом, так как имеет сравнительное преимущество в производстве второго товара. Третий случай, когда страна имеет такие же альтернативные издержки производства товара, что и у её торгового партнера. Тогда, как и в первом случае, максимальное количество потребляемого товара с учётом торговли и без неё будет одинаковым.
По условию, максимальное количество кукурузы, которое может произвести Антигуа равно 100, что меньше максимального количества кукурузы на КТВ Барбуды. Это означает, что Барбуда не может закупить всю кукурузу у Антигуа и добиться потребления, равного 102 початкам, и тогда максимальное количество кукурузы, которое может произвести Барбуда равно 102, так как только при таком условии КТВ острова может оставаться линейным.
в) ( 10 баллов) Предположим, что острова объединились в одну страну. Какое максимальное количество кукурузы она может произвести? Схематично изобразите КПВ объединённой страны и отметьте все известные точки на графике.
Из предыдущего пункта известно, что максимальное количество кукурузы, которое может произвести Барбуда равно 102, а максимальное количество Антигуа — 100. Таким образом, при объединении островов их предельное количество произведенных початков составит 202.
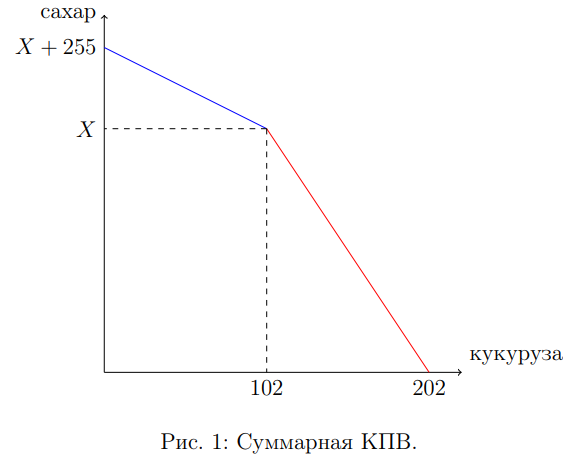
В пункте б) было показано, что Антигуа не может обладать сравнительным преимуществом в производстве кукурузы. Это означает, что если объединенный стране необходимо произвести не более 102 початков кукурузы, то производство кукурузы будет происходить только на острове Барбуда, а все мощности острова Антигуа будут направлены на производство сахара, что даёт синий участок на рисунке 1. В случае, когда кукурузы необходимо более 102 початков, то остров Барбуда будет производить только кукурузу в размере 102 початка, а оставшиеся необходимые початки произведёт Антигуа, что даёт красный участок на рисунке 1. Мы выяснили, что максимальное количество кукурузы, которое объединенная страна может произвести равно 202. А в точке излома КПВ координаты будут равны (102;X), при этом X невозможно определить из данных задачи, однако максимальное количество производимого сахара будет на 255 кг больше.