Какой товар, такие и издержки
Компания «Ёлки-иголки» занимается производством новогодних ёлок. На недавнем собрании обсуждались неудачные продажи в этом году: прибыль была отрицательной и составила − 5 условных единиц. Компания необычная, её кривая предельных издержек имеет нестандартный вид:
MC = \begin{cases} 20 - 2Q, & 0 \leq Q \leq 5 \\ \frac{7Q}{10} - \frac{1}{2}, & 5 < Q \leq 15 \\ 30 - Q, & 15 < Q \leq 20 \\ \frac{2Q}{5}, & 20 < Q \leq 25 \\ 20, & Q > 25 \end{cases}
Кривая предельной выручки также имеет похожий специфический вид:
MR = \begin{cases} 2Q, & 0 \leq Q \leq 5 \\ \frac{41}{2} - \frac{7Q}{10}, & 5 < Q \leq 15 \\ Q - 10, & 15 < Q \leq 20 \\ 20 - \frac{2Q}{5}, & 20 < Q \leq 25 \\ 0, & Q > 25 \end{cases}
Причины столь плохих результатов были выявлены почти сразу: главный экономист компании пропускал лекции по микроэкономике в университете и что-то слышал про правило MR = MC, но совершенно не умеет им пользоваться. К тому же он перепутал графики MR(Q) и MC(Q)!
Совет сразу же уволил его и открыл вакансию нового главного экономиста, на которую Вы теперь претендуете. Все кандидаты должны решить следующие задачи (фирма может продавать нецелое количество ёлок: кому-то нужны только иголки):
- (5 баллов) Изобразить правильный график предельных издержек и предельной выручки.
- (7 баллов) Найти количество ёлок, которое фирма произвела в прошлом году.
- (13 баллов) Посчитав ожидаемую прибыль от выбранного им выпуска, бывший главный экономист решил воспользоваться правилом «Если нет разницы – зачем производить больше?». Сколько произвела фирма по его совету с учётом этого правила?
- (5 баллов) На сколько нужно изменить выпуск, чтобы наконец-то производить оптимальное количество ёлок (в сравнении с пунктом 3)? Какую прибыль получит фирма при таком выпуске?
а) Для начала построим график издержек: (3 балла)
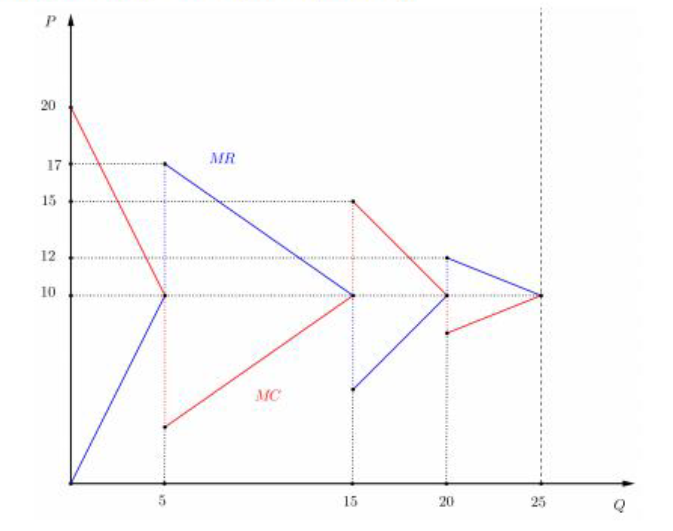
Примечание: за неточности в графиках возможно снятие 1-2 баллов в зависимости от ошибки.
б) Вполне очевидно, что фирма зарабатывает, когда график MR выше, чем MC, и терпит убытки, когда все наоборот.
За идею о вычислении прибыли - 2 балла
Можно найти, сколько фирма будет зарабатывать. Для этого рассчитаем площади между кривыми MR и MC.
S_1=50,S_2=70,S_3=25,S_4=10
За непосредственное вычисление прибыли в точках MR=MC - 3 балла.
Теперь посмотрим, какие прибыли могла получать фирма в точках MR=MC.
\pi(Q) = \begin{cases} -50, & Q = 5 \\ 20, & Q = 15 \\ -5, & Q = 20 \\ 5, & Q = 25 \end{cases}
За вывод о том, что Q*=20 −1 балл.
Значит, в этом году фирма производила Q=20 елок.
Примечание: возможно решение через вычисление функций общей выручки и общих издержек, НО стоит понимать, что по функции MR можно восстановить TR только с точностью до константы, которая будет различна на всех предложенных отрезках.
в)
Если экономист решил воспользоваться правилом «Если нет разницы – зачем производить больше», то он должен был найти уровни выпуска, приносящие такую же прибыль, и выбрать наименьший из них. Проще всего это сделать нарисовав график прибыли и прямую \pi=-5, и найдя значение выпуска в точке с наименьшим Q.

Нам подходят первые две точки, (в третьей точке MR=MC). Но по условию задачи мы должны брать минимальное Q, поэтому правильным ответом будет Q_1 = 5 - \frac{3\sqrt{10}}{2}, которое можно вычислить как площадь трапеции.
Пусть при произвольном Q* площадь между кривыми MC и MR будет равна 5, тогда S = \frac{Q^*(20 - 4Q^*)}{5} = 5, решив квадратное уравнение и отбросив больший корень находим правильный ответ: Q^* = 5 - \frac{3\sqrt{10}}{2}.
За вычисление правильного ответа - 5 баллов.
За обоснование того, что это именно он (сравнить со значением во второй точке или показать через график выше) - 3 балла
г) Из предложенного выше решения видно, что оптимальным выпуском для фирмы является Q*=15, в этой точке фирма заработает \pi=20. Тогда фирме нужно увеличить свой выпуск на 10 + \frac{3\sqrt{10}}{2}
За определение оптимального количества - 2 балла
За вычисление правильного ответа - 1 балл
Примечание:
Задача стоила 30 баллов в 8-9 классах и 20 баллов в 10-11 классах