Воды нет. Растительности нет. Населена роботами
На планете Шелезяка живёт две группы роботов: 100 современных и 100 устаревших. Капитан Зелёный на старости лет решил открыть частную клинику на планете Шелезяка и оказывать платные медицинские услуги живущим там роботам. Суммарные спросы на медицинские услуги у обеих групп разные. Для устаревших роботов функция спроса может быть представлена в виде P_1(Q_1)=6-Q_1/200, а для современных — P_2(Q_2)=6-Q_2/100, соответственно, где P_i — цена одной починки (в д.е.), а Q_i — суммарное количество починок для i -той группы роботов, индивидуальный спрос внутри каждой группы одинаковый. Предельные издержки Капитана Зелёного постоянны и равны 2, постоянные издержки отсутствуют. Капитан Зелёный — единственный продавец услуг по починке роботов на планете. Капитан Зелёный не может назначать разные цены для отдельных групп покупателей. Считайте, что количество починок и цены могут быть нецелыми.
а) ( 5 баллов) Какое количество услуг он продаст в равновесии и по какой цене?
Для начала заметим, что как для современных, так и для устаревших роботов максимальная цена за один билет равняется 6, что говорит о том, что при наших функциях спроса будут покупать при фиксированной цене ненулевое количество ремонтов обе группы.
Теперь выразим суммарную обратную функцию спроса обеих групп
Q = Q_1 + Q_2 = 1200 - 200P + 600 - 100P = 1800 - 300P.
Постоянные издержки Капитана нулевые, а предельные издержки постоянны и равны 2, то TC=2Q. Таким образом запишем функцию прибыли
\pi = QP - TC = (1800 - 300P)P - 2(1800 - 300P) = 2400P - 300P^2 - 3600.
Это парабола ветвями вниз, максимум в вершине
P^{*} = \frac{-b}{2a} = \frac{2400}{600} = 4.
Тогда Q=1800-300*4=600. При этом \pi=1200>0.
б) ( 20 баллов) Капитан Зелёный решил ввести специальный медицинский полис для покупателей, который позволит получать им услуги клиники на 20\% дешевле. За каждый купленный полис каждый покупатель платит Капитану стоимость полиса равную 1,75 д.е. Капитан может установить новую цену на свои услуги. После объявления новой цены и стоимости полиса каждый робот решает, будет он покупать полис или нет, максимизируя свой потребительский излишек. Какую цену установит Капитан на свои услуги?
Возможны несколько случаев.
1. Все роботы покупают полис.
2. Никто из роботов не покупает полис.
3. Только современные роботы покупают полис.
Случай, когда только современные роботы покупают полис, не будет отдельно рассматриваться, т.к. функция спроса устаревших роботов лежит строго выше современных, и если современные роботы захотят купить полис, то и устаревшие тоже захотят его купить.
Рассчитаем излишки потребителей (рисунок 1 ) до ( CS_{C,0} и CS_{Y,0} ) и после ( CS_{C,1} и CS_{Y,1} ) покупки полиса (в расчете на 1 робота). Для современного робота
CS_{C,0} = (6 - P)^2 \cdot \frac{1}{2}, \qquad CS_{Y,1} = (6 - 0{,}8 \cdot P)^2 \cdot \frac{1}{2} - 1{,}75.
Для устаревшего робота
CS_{Y,0} = (6 - P)(12 - 2P) \cdot \frac{1}{2} = (6 - P)^2, \qquad CS_{Y,1} = (6 - 0{,}8 \cdot P)^2 - 1{,}75
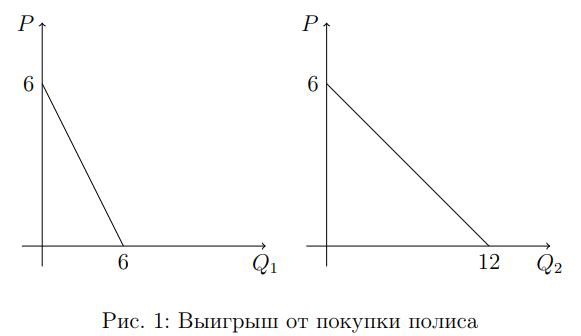
1. Все роботы покупают полис.
\pi = (0{,}8P \cdot Q(0{,}8P) - 2 \cdot Q(0{,}8P)) + 1{,}75 \cdot 200 \to \max_{0{,}8P}.
Мы уже решали эту оптимизационную задачу для 0,8P в пункте а).
0{,}8P^{*} = 4 \Rightarrow P^{*} = 5.
Посмотрим, захотят ли отклониться устаревшие роботы
CS_{C,1} < CS_{C,0},
(6 - 0{,}8 \cdot 5)^2 \cdot \frac{1}{2} - 1{,}75 < (6 - 5) \cdot \frac{1}{2} б
0{,}25 < 0{,}5.
Значит, устаревшие роботы при такой цене не захотят покупать полис. Найдем точку, при которой устаревшим роботам будет все равно, покупать полис или нет
CS_{C,1} = CS_{C,0},
(6 - 0{,}8 \cdot P)^2 \cdot \frac{1}{2} - 1{,}75 = (6 - P) \cdot \frac{1}{2},
P = \frac{20 \pm 5\sqrt{2}}{6}.
Мы получили 2 цены из решения квадратного уравнения, одна из них ближе к точке оптимума, чем другая (рисунок 2 ), она и будет оптимальной в этом случае.
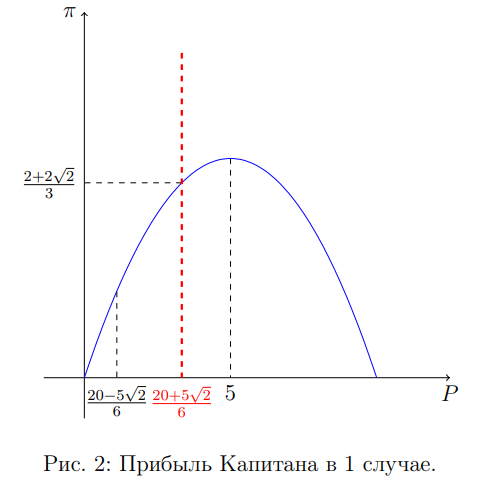
Вычислим прибыль Капитала от продажи полиса обеим группам
\pi = \frac{1}{3}(2 + 2\sqrt{2})(10 - 2\sqrt{2}) \cdot 100 + 350 \approx 1504{,}25 > 1200.
2. Никто из роботов не покупает полис.
Оптимальная цена в этом случае такая же, как и в пункте а). Рассмотрим, захочет ли кто-то отклониться
Устаревшие роботы
(6 - 4)^2 \cdot \frac{1}{2} < (6 - 0{,}8 \cdot 4)^2 \cdot \frac{1}{2} - 1{,}75
4<6,09
Значит, если устаревшие роботы хотят купить полис, то и современные тоже. Тогда, чтобы никто не покупал полис, Капитану придется повышать цены, отходя от точки оптимума P=4, тем самым уменьшая свою прибыль. Этот случай точно не оптимальный, потому что Капитан может воспользоваться стратегией из случая 1 и увеличить свою прибыль.
3. Только устаревшие роботы покупают полис.
\pi = ((P - 2)(6 - P)) + (0{,}8P - 2)(12 - 2 \cdot 0{,}8P) + 1{,}75 \cdot 100 = (-2{,}28P^2 + 20{,}8P - 34{,}25) \cdot 100.
Это парабола ветвями вниз, максимум в вершине, тогда P^{*} = \frac{260}{57} \approx 4{,}58.
В первом случае мы уже выяснили, что если P > \frac{20 + 5\sqrt{2}}{6} \approx 4{,}51, то современные роботы не захотят покупать полис.
Пока не будем проверять, будут ли покупать полисы устаревшие роботы. Найдем прибыль Капитана
\pi = \frac{75175}{57} \approx 1318 < 1504{,}25
Таким образом, даже если устаревшие роботы и правда захотят купить полис, то Капитан все равно воспользуется стратегией из случая 1 и назначит цену, равную
P = \frac{20 + 5\sqrt{2}}{6}.