Вмешательство Лернера
Монополист работает на рынке со спросом и несёт издержки . Государство, недовольное монопольным положением фирмы, рассматривает два варианта вмешательства на рынок:
Назначить монополисту фиксированный штраф , если индекс Лернера в точке равновесия монополиста превышает . При этом государство, зная предельные издержки монополиста, вычисляет индекс Лернера как , где — цена, установленная фирмой, а — значение предельных издержек в точке оптимального выпуска.
Обратите внимание, что в случае такого вмешательства монополист не обязан устанавливать цену, соответствующую спросу.
Государство устанавливает предельное превышение цены, установленной монополистом, над ценой, равной , по ставке . Таким образом, если монополист устанавливает цену и , то монополист обязан заплатить фиксированный штраф по ставке . Предполагается, что при прочих равных условиях монополист предпочитает выбрать монопольный выпуск. Государство самостоятельно выбирает уровень и .
( баллов) Определите максимальные сборы государства в каждом из случаев. Какой вид вмешательства выберет государство, если его цель — максимизация сборов?
Определим, какое количество товара и по какой цене будет продаваться на рынке. Решить задачу максимизации прибыли монополиста можно двумя способами.
Способ . Функция предельной выручки монополиста задается как , функция предельных издержек задается как . Предельные издержки возрастают по , предельная выручка убывает по , тогда оптимумом монополиста является точка пересечения и .
.
Способ . Запишем прибыль монополиста: . Заметим, что прибыль монополиста — парабола ветвями вниз, значит максимум в вершине: .
Найдем прибыль монополиста, если государство никак не вмешивается на рынок: .
Найдем индекс Лернера в точке равновесия, в случае отсутствия вмешательства государства: .
Рассмотрим первый вариант вмешательства (штраф если индекс Лернера превышает ). В точке индекс Лернера превышает .
Если монополист не платит штраф, то он выбирает такие количества и цену, чтобы индекс Лернера будет меньше или равен , то есть:
.
Если монополист выбирает не платить штраф, но максимизирует свою прибыль, то при любом выберет наибольшую цену, удовлетворяющую ограничению и лежащую не выше спроса.
Найдем, при каких значениях монополист будет выбирать точку на спросе:
Цена, которая установится на рынке, если монополист продает единиц:
Прибыль монополиста в этом случае:
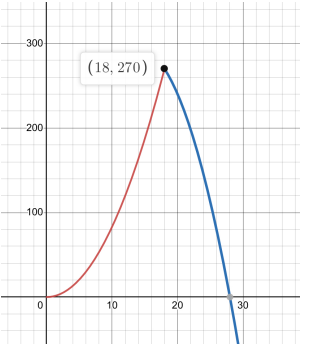
Максимум функции прибыли достигается в точке
Прибыль в этой точке равна
Монополист выбирает и такие, что индекс Лернера не больше , только если прибыль без уплаты штрафа не больше прибыли со штрафом:
Рассмотрим второй вариант вмешательства. Запишем прибыль монополиста как функцию от цены и будем искать максимум прибыли при ограничении , то есть такие значения цены, при которых монополисту не нужно будет платить штраф
Цена, если бы не было ограничения, была бы равна и так как всегда не больше , то .
При введении штрафа монополист будет готов заплатить штраф только если , где — максимальная прибыль монополиста в отсутствии любого государственного вмешательства, — прибыль монополиста, если государство выбирает второй вариант государственного вмешательства.
Так как государство максимизирует сборы, то неравенство выполняется как равенство
Государство одновременно выбирает и , и , тогда оно выберет такое , чтобы максимизировать , так как задачей государства является максимизация суммы штрафов. Таким образом государство будет стремиться минимизировать .
Так как государство стремится добиться минимальной прибыли монополиста при помощи потолка , то оно будет ставить минимальное значение , так как при этом государство максимально ограничивает монополию, тем самым минимизируя прибыль монополиста. То есть при каждом прибыль монополиста при потолке – меньше прибыли монополиста при потолке – при любых .
Если монополист не хочет платить штраф , то установит цену . Найдем количество товара , которое максимизирует прибыль монополиста при цене
Это парабола ветвями вниз, максимум в вершине:
Это значение выпуска подходит под ограничение.
Прибыль монополиста равна:
Тогда государство установит штраф на уровне
Государство выберет второй вариант вмешательства, так как он приносит большую сумму штрафов.
( баллов) Почему введение меры может быть затруднительно в реальном мире?
Введение первой меры может быть затруднительным, так как государство не всегда наблюдает предельные издержки монополиста.
( баллов) Почему государство на практике не максимизирует величину штрафов?
Государство не максимизирует величину штрафов, потому что смысл штрафа в сдерживании определенного поведения. Если штрафы выплачиваются, то нежелательное поведение не сдерживается.