Валютный арбитраж и немного фантастики
Мошики – национальная валюта страны МОШ, а вошики и очики – денежные единицы двух
соседних дружественных государств. Сейчас ( 2 марта 2025 года) у юного Марти имеются наличные деньги в трёх валютах: 13000 мошиков, 2000 вошиков и 1000 очиков, но Марти хочет потратить их не сегодня, а через год. Расходы он планирует в мошиках, поэтому стремится, чтобы итоговая сумма была наибольшей при переводе её именно в эту валюту.
«МОШбанк» – единственный надёжный банк в МОШе – предлагает своим клиентам сделать срочный вклад на год в мошиках, вошиках или очиках на следующих условиях:
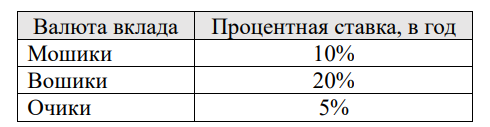
В «МОШбанке» Марти может открыть депозиты в любой из указанных валют (Марти может открыть депозит в одной валюте или несколько депозитов в разных), но через год ( 2 марта 2026 года) он должен будет снять деньги со всех депозитов и перевести их в мошики.
Валютообменными операциями в стране МОШ занимается также только «МОШбанк».

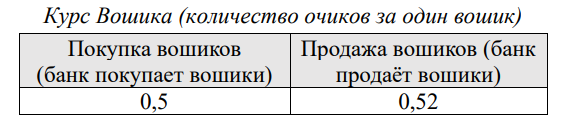
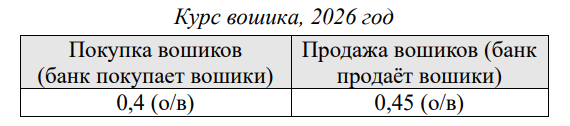
Недавно Марти ненадолго оказался в будущем и случайно захватил с собой газету, в которой опубликованы курсы валют на 2 марта 2026 года.

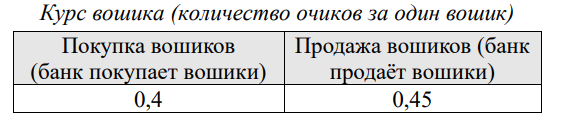
1. Определите, какая максимальная сумма в мошиках может быть у Марти в результате правильно выбранной стратегии (докажите, что выбранная вами стратегия является оптимальной, и, если у Марти имеется несколько оптимальных стратегий, покажите все).
2. Определите и обоснованно покажите, при какой минимальной процентной ставке по депозиту в вошиках Марти целесообразно сберегать в этой валюте (если цель Марти не меняется – он попрежнему хочет максимизировать сумму в мошиках через год)?
Справочно (знания термина не требовалось для решения задачи).
Арбитраж – несколько последовательных сделок, направленных на извлечение прибыли из-за разницы в ценах.
Валютный арбитраж – покупка и продажа валют с последующим совершением обратной сделки (в том числе через другие валюты) с целью получения прибыли за счет разницы в валютных курсах.
Обозначение курсов валют с единицами измерения (не требуется для решения, но может облегчить перевод из одной валюты в другую):

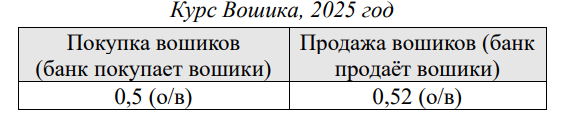

Для облегчения понимания при решении задачи каждую валюту мы будем обозначать заглавной буквой её названия ( М, \ В, \ О ).
Пункт 1 задачи ( 58 баллов)
Рассмотрим, может ли Марти заработать на валютном арбитраже в 2025 году. Для этого будем рассматривать сумму x каждой валюты и определять, сколько денег в исходной валюте будет после цепочки обменов.
1) Проверим очевидные цепочки:
\text{M--B--M:}\qquad x \mapsto \frac{x}{13} \mapsto \frac{12x}{13} < x
\text{M--O--M:}\qquad x \mapsto \frac{x}{25} \mapsto \frac{24x}{25} < x
\text{O--B--O:}\qquad x \mapsto \frac{x}{0.52} \mapsto \frac{0.5x}{0.52} < x
\text{B--O--B:}\qquad x \mapsto 0.5x \mapsto \frac{0.5x}{0.52} < x
Вывод: арбитраж данным способом невозможен
5 баллов: 1 балл за каждую цепочку и 1 балл за вывод
Если явно обоснованно указать, что во всех четырёх случаях «МОШбанк» покупает любую валюту дешевле, чем продаёт ее, поэтому заработать не удаётся, также выставляется 5 баллов.
2) Рассмотрим, удастся ли арбитраж через другую валюту:
\text{B--O--M--B:}\qquad x \mapsto 0.5x \mapsto 24\cdot 0.5x \mapsto \frac{24\cdot 0.5x}{13}=\frac{12x}{13}<x.
\text{B--M--O--B:}\qquad x \mapsto 0.5x \mapsto \frac{x}{25} \mapsto \frac{12x}{13}<x
\text{O--B--M--O:}\qquad x \mapsto \frac{x}{0.52} \mapsto \frac{12x}{0.52} \mapsto \frac{12\cdot 100x}{0.52\cdot 25}=\frac{48x}{52}<x
\text{O--M--B--O:}\qquad x \mapsto 24x \mapsto \frac{24x}{13} \mapsto \frac{24\cdot 0.5x}{13}=\frac{12x}{13}<x
\text{M--B--O--M:}\qquad x \mapsto \frac{x}{13} \mapsto \frac{0.5x}{13} \mapsto \frac{24\cdot 0.5x}{13}=\frac{12x}{13}<x
\text{M--O--B--M:}\qquad x \mapsto \frac{x}{25} \mapsto \frac{x}{25\cdot 0.52} \mapsto \frac{12x}{25\cdot 0.52} =\frac{12\cdot 100x}{25\cdot 52}=\frac{48x}{52}<x
Вывод: арбитраж в 2025 году невозможен
15 баллов: по 2 балла за каждую цепочку и 3 балла за вывод
3) Если в 2026 существует возможность заработать на разнице курсов валют и, следовательно, получить бесконечно большую сумму за счёт валютного арбитража, необходимо сначала рассмотреть такую возможность (максимально 34 балла):
Через два обмена одной валюты
\text{M--B--M:}\qquad x \mapsto \frac{x}{12} \mapsto \frac{11.5\,x}{12} < x
\text{M--O--M:}\qquad x \mapsto \frac{x}{25.5} \mapsto \frac{25\,x}{25.5} < x
\text{O--B--O:}\qquad x \mapsto \frac{x}{0.45} \mapsto \frac{0.4\,x}{0.45} < x
\text{B--O--B:}\qquad x \mapsto 0.4x \mapsto \frac{0.4\,x}{0.45} < x
4 балла: 1 балл за каждую цепочку
4) Через третью валюту. В данном случае финальным обменом по условию должен быть обмен на Мошики. Если перевод осуществляется из Очиков или Вошиков, необходимо сравнить результаты цепочки и результат однократного обмена на Мошики:
\text{B--O--M:}\qquad x \mapsto 0.4x \mapsto 25.5\cdot 0.4x = \frac{102x}{10}=10.2x < 11.5x
\text{O--B--M:}\qquad x \mapsto \frac{x}{0.45} \mapsto \frac{11.5x}{0.45} = \frac{1150x}{45}=\frac{230x}{9} > 25x
Вывод: Очики выгоднее переводить в Мошики через Вошики, это позволит получить в итоге больше мошиков больше, чем прямой обмен
8 баллов: по 2 балла за анализ каждой цепочки, 4 балла за вывод
5) Тогда рассмотрим схожую цепочку обмена, которая начинается с мошиков и осмотрим, можно ли на этом заработать:
\text{M--O--B--M:}\quad x \mapsto \frac{x}{25.5} \mapsto \frac{x}{25.5\cdot 0.45} \mapsto \frac{11.5x}{25.5\cdot 0.45} = \frac{115\cdot 100\,x}{255\cdot 45} = \frac{23\cdot 20\,x}{51\cdot 9} = \frac{460x}{51\cdot 9} = \frac{460x}{459} > x
Вывод: имея любую сумму в мошиках, можно в итоге получить большую сумму в мошиках
8 баллов: 2 балла за анализ цепочки, баллов за вывод
6) Имея изначально сумму в вошиках, можно перевести её в мошики и зарабатывать:
\text{B--M--O--B--M:}\quad x \mapsto 11.5x \mapsto \frac{11.5x}{25.5} \mapsto \frac{11.5x}{25.5\cdot 0.45} = \frac{115\cdot 100\,x}{255\cdot 45} = \frac{23\cdot 20\,x}{51\cdot 9} = \frac{460x}{51\cdot 9} = \frac{460x}{459} \mapsto \frac{11.5\cdot 460x}{459} > 11.5x
10 баллов: 2 балла за анализ цепочки, 8 баллов за вывод
7) Имея изначально сумму в очиках, можно перевести ее в мошики (через вошики) и зарабатывать (схема О – В – М – О – В – М )
4 балла за вывод
Общий вывод: из-за возможностей арбитража сумма, которую может заработать Марти, может быть бесконечно большой.
8) Размер процентной ставки не имеет значения, так как мы показали, что при любом доходе от депозита можно заработать в 2026 году на разнице в валютных курсах бесконечно большую сумму.
4 балла за указание
Пункт 2 задачи ( 2 балла).
С учетом верного решения пункта 1 Марти безразлично, в какой валюте сберегать. Поэтому он может сберегать в вошиках при любой ставке.