Задача 1.1.3
В стране ФЭШН производятся два товара: задачи (x) и лекции (y). Технологии производства задач и лекций описываются следующими соотношениями: x=L_x^2, y=L_y^2, где x, \ y — количества произведённых товаров, а L_x, \ L_y — количества труда, затраченные на производство задач и лекций соответственно. Суммарные запасы труда страны равны 2. На мировом рынке образования цена одной задачи равна цене одной лекции.
а) Определите уравнение КТВ страны
\\ \\ \\ Отбор в Экономическую Школу ФЭН, 2022
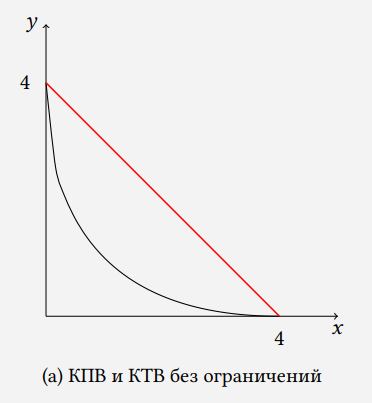
Выразим L_x=\sqrt x, L_y=\sqrt y и подставим эти зависимости в ограничение по труду: \sqrt x+\sqrt y=2. Мы получили уравнение КПВ, можем нанести на график: рис. a (черный).
Наносим на график карту изовыручек TR=x+y. Наивысшее касание МПВ с одной из кривых торговых возможностей проходит через точку (0, \ 4), поэтому КТПВ в первом пункте будет выглядеть следующим образом: x+y=4.
б) Руководитель страны Александр оказался недоволен получившимся результатом торговли, поэтому запретил ввозить и вывозить из страны более одной единицы любого товара. Например, обменять 0,75 единиц лекций на 0,75 единиц задач можно, а вот 1,25 единиц лекций на 1,25 единиц задач уже нельзя. Выполните задание предыдущего пункта при данном условии. Проиллюстрируйте полученную кривую графически.
В этом пункте КТВ можно строить векторным методом (это не единственный метод решения). Каждую точку КПВ можно сдвинуть сначала на вектор a(1, \ -1) при всех значениях a от 0 до 1, а затем на противоположный вектор a(-1, \ 1). Координаты вектора означают количества товаров, которые приобретаются или продаются. Если координата вектора, на который сдвигается точка положительная, значит товар приобретается, если отрицательная — товар продаётся. Параметр a отвечает за то, какую
долю от импортной/экспортной квоты использует транзакция. Точно так же к КТВ можно относиться и в предыдущем пункте, но там данное усложнение не требуется. Нарисуем это на графике: рис. b. Кривые в отрицательных областях нарисованы для наглядности.
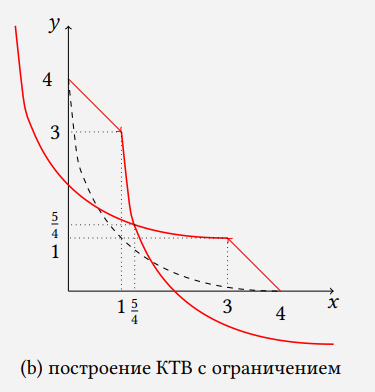
Берём верхнюю огибающую. Точку пересечения двух частей графика получаем, решая систему иррациональных уравнений. Сами уравнения этих частей получаем используя сдвиг графиков уравнений: f(x-a, \ y-b)=2, где a — сдвиг по горизонтали, b — сдвиг по вертикали:
\begin{cases} y = 4 - x, & x \in [0; 1] \text{ или } x \in [3, 4] \\ \sqrt{y} + 1 + \sqrt{x - 1} = 2, & x \in (1, \frac{5}{4}] \text{ и } y \in [\frac{5}{4}, 3) \\ \sqrt{y} - 1 + \sqrt{x + 1} = 2, & x \in (\frac{5}{4}, 3) \text{ и } y \in (1, \frac{5}{4}) \end{cases}