Знахарь и злой дух. Олимпиада Колокольникова 1 тур 2025 (7-8 класс)
Знахарь Ефимыч может собирать грибы (x) и ягоды (y). Ефимыч знает, как грибы и ягоды нужны лесу, но при этом сам вынужден собирать их для своих лечебных отваров, поэтому его функция полезности равна:
U(x, \ y)=100-(x-12)^2-(y-8)^2
а) ( 3 балла) При каких x и y достигается максимальная полезность знахаря U_{max} ?
Проанализируем функцию полезности знахаря. Так как любое t^2\geq 0, то (x-12)^2\geq 0 и (y-8)^2\geq 0, но мы вычитаем эти неотрицательные выражения из 100, значит, 100-(x-12)^2-(y-8)^2 точно не больше 100, и тогда максимальная полезность будет равна 100, причем это возможно только, если (x-12)^2=0 и (y-8)^2=0. Получаем x=12 и y=8.
Ответ: x=12 и y=8.
б) ( 3 балла) За день у него хватает времени, чтобы собрать не больше 20 грибов, при этом каждый гриб искать приходится в k>0 раз дольше, чем каждую ягоду. Найдите все такие значения k, что знахарь может достичь своей максимальной полезности U_{max}, которую вы нашли в предыдущем пункте.
В лесу появился злой дух, который хочет испортить жизнь знахарю. После того как Ефимыч соберет грибы и ягоды, он может наложить на знахаря заклятие изменения, из-за чего все грибы станут ягодами, а ягоды — грибами. Дух старается сделать полезность знахаря как можно меньше. Если злому духу безразлично накладывать заклятие или нет, он предпочитает не делать этого. Ефимыч знает о существовании духа и о том, что тот пытается уменьшить его полезность.
Знахарю для максимальной полезности необходимо собрать 12 грибов и 8 ягод. Один гриб искать в k раз дольше, чем одну ягоду, значит, за одно и то же время он успеет собрать в k раз больше ягод, чем грибов. Пусть он нашел y ягод, значит, он отказался от \frac{y}{k} грибов. Тогда количество собранных грибов x\leq 20-\frac{y}{k}.
Получаем, что для достижения максимальной полезности:
12\leq 20-\frac{8}{k}
\frac{8}{k}\leq 8
8\leq 8k (так как k>0 )
8k\geq 8
k\geq 1
Ответ: k\geq 1.
в) ( 5 баллов) При k=1 определите, сколько ягод и грибов нужно собрать знахарю, чтобы достичь наибольшей полезности за один день.
При k=1 получаем x\leq 20-\frac{y}{1}, то есть x+y\leq 20.
Если заклятие есть: U_з(x, \ y)=100-(y-12)^2-(x-8)^2.
Если заклятия нет: U_{бз}(x, \ y)=100-(x-12)^2-(y-8)^2.
Если подставить x\leq 20-\frac{y}{1} в выражения прибыли, то получим:
U_з(y) \leq 100 - (y-12)^2 - ((20-y)-8)^2 = -2y^2 + 48y - 188
U_{бз}(y) \leq 100 - ((20-y)-12)^2 - (y-8)^2 = -2y^2 + 32y - 28
Заметим, что итоговой полезностью знахаря будет нижняя огибающая этих двух парабол, тогда график этих двух парабол будет иметь следующий вид:
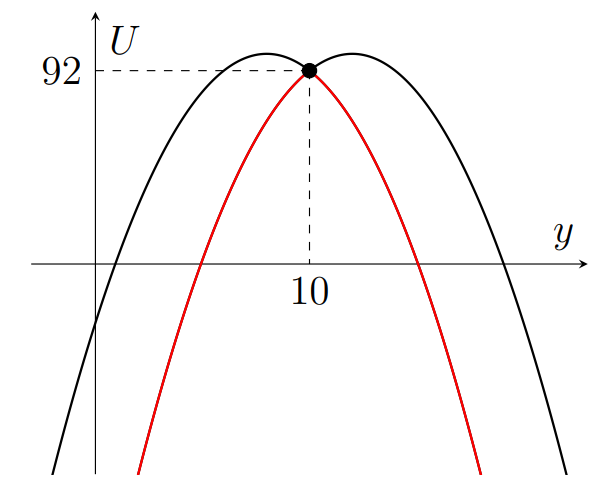
Свой максимум нижняя огибающая достигает в точке пересечения двух парабол:
-2y^2+48y-188=-2y^2+32y-28
y=10
Так как точка максимальной полезности находится на параболах, для нахождения оптимального x можно считать, что полученное ранее неравенство в данном случае равенство: x=20-y=10
Оптимальную точку x=y=10 можно было также и угадать, но в таком случае необходимо привести доказательство того, что при таких значениях действительно достигается максимальное значение полезности: пусть x=10+a, тогда y=10-a. В таком случае полезность будет равна U_з(x, \ y)=100-(-2-a)^2-(2+a)^2 или U_{бз}(x, \ y)=100-(-2+a)^2-(2-a)^2. Перепишем по-другому и получим U_з(x, \ y)=100-8-8a-2a^2 или U_{бз}(x, \ y)=100-8+8a-2a^2.
Тогда, если a>0, то дух выберет U_з(x, \ y)=92-8a-2a^2<92, если же a<0, то дух выберет U_{бз}(x, \ y)=100-8+8a-2a^2<92, а значит, x=y=10 и U=92 это оптимум.
Ответ: x=y=10.
г) ( 1 балл) Наложит ли злой дух заклятие на знахаря при такой стратегии?
При стратегии (10, \ 10) полезность Ефимыча равна 92 независимо от того, наложено заклятие или нет. Злой дух не может уменьшить полезность знахаря, поэтому ему нет смысла накладывать заклятие.
Ответ: нет, не наложит.