Оптимальная цена при неизвестном спросе
Некоторая фирма-монополист хотела бы установить цену, максимизирующую выручку, однако функция спроса D(p) известна фирме лишь примерно (что соответствует реальности для боль-
шинства фирм). А именно, фирма знает, что для каждой цены выполнено
а также что при p>26 спрос равен нулю. Другой информации о функции спроса нет. В частности, она необязательно линейна.
Какие значения может принимать цена, при которой выручка фирмы максимальна?
Ответ
Если бы функция спроса проходила по нижней границе 24−p, оптимальная цена равнялась бы 12, а если по верхней границе 26−p, то 13. Поэтому естественно предположить, что оптимальная цена может принимать лишь значения от 12 до 13. В действительности, это не так. Обозначим истинную функцию выручки за . Нам известно, что . До нижеприведенного решения можно додуматься, если построить графики функций p(24−p) и p(26−p) (см. рис. 5.1) и попытаться вписывать разные графики между этими двумя параболами.
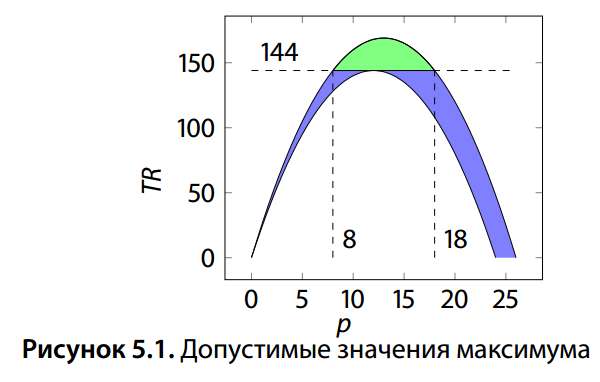
Докажем, что оптимальная цена не может быть меньше 8. Действительно, назначая цену p<8, фирма в лучшем случае получит выручку . Если же фирма
назначит цену 12, она получит не меньше, чем . Значит, любая цена, меньшая 8, не может быть оптимальна.
Аналогично, если фирма назначит цену p>18, она в лучшем случае получит выручку . Если же фирма назначит цену 12, она получит не меньше, чем . Значит, любая цена, большая 18, не может быть оптимальна.
Наконец, покажем, что любая цена из отрезка [8; 18] может быть оптимальной для какой-то функции спроса D(p), удовлетворяющей условию. Вообще говоря, для каждой цены можно привести «свой» пример функции спроса , такой, что является оптимальной ценой при спросе . Однако в данной задаче существует единый пример, который покрывает сразу все цены из отрезка [8; 18]. Рассмотрим функцию спроса
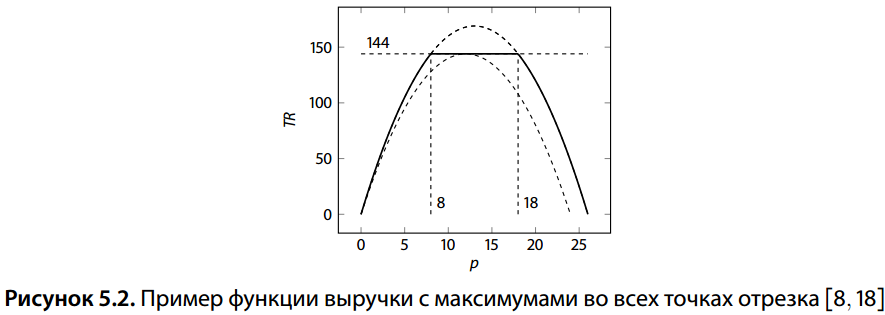
Легко проверить, что и при этом для данной функции спроса оптимальными являются все цены от 8 до 18 (см. рис. 5.2).
Ответ:
.