Задача 1.1.1
В каждом из двух регионов закрытой страны производят товары X и Y. Альтернативные издержки производства в каждом из регионов постоянны, положительны и конечны. Предпочтения жителей страны изначально были таковы, что вместе с единицей товара X они хотели потреблять 3 единицы товара Y, а затем предпочтения изменились так, что теперь X и Y потребляются в пропорции 1 к 2. При описанном изменении объёмы потребления товаров изменились: Y на 3 единицы, а X на 1 единицу. Определите диапазон возможных значений X(14), где функция X(Y) описывает КПВ страны, если при описанных изменениях в стране изменилось число регионов, где производится только товар Y.
\\\\
\\ Экономический биатлон, Летний ЛОС(ь) 2024
Кривая комплектов сдвинулась с положения y=3x в положение y=2x. Пусть (x_0, \ y_0) — изначальная точка производства в стране. Понятно, что объём X мог лишь увеличиться, а Y — сократиться. Составим систему уравнений:
\begin{cases} y_0 = 3x_0 \\ y_0 - 3 = 2(x_0 + 1) \end{cases}
Получаем координаты изначальной и конечной точек производства: x_0=5, \ y_0=15, \ x_1=6, \ y_1=12. Эти точки, лежат на КПВ страны.
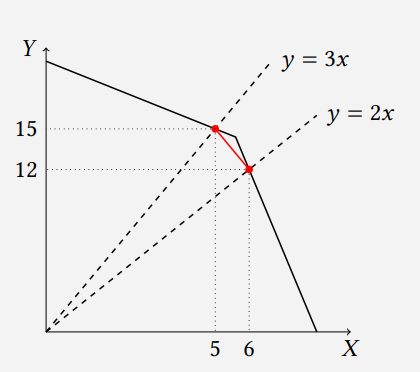
КПВ представляет собой кусочно-линейную кривую. Так как при описанных изменениях в стране изменилось число регионов, где производится только товар Y, а объём производства X увеличился, то точка производства переместилась с верхнего участка КПВ на нижний (рис. 1). Изначальная точка также могла оказаться точкой излома. Наклоны каждого из участков КПВ могут меняться, но при этом КПВ не может быть выпуклой, поэтому самое нижнее положение КПВ на отрезке x\in[5, \ 6] — это отрезок, соединяющий изначальную и конечную точки. Уравнение, описывающее этот отрезок: y=15-3(x-5). Значению y=14 соответствует x=16/3. Это левая граница X(14). Правая граница — это X=6, достигаемая при устремлении наклона нижнего участка к бесконечности. Левая граница включена в ответ, правая — не включена, так как альтернативные издержки конечны.
Ответ: X(14)\in[16/3, \ 6).