Задача 1.2.6. Скучная задача, где всего лишь надо сложить заводы
У фирмы в распоряжении есть два завода с непрерывными функциями издержек. На одном заводе функция предельных издержек имеет вид
MC_1(q_1) = \begin{cases} 10q_1, & q_1 \leq 10 \\ 5q_1, & q_1 > 10 \end{cases}
А на втором заводе функция предельных издержек имеет вид MC_2=75. «Сложите» данные заводы.
\\ \\ Экономическая школа ФЭН, контрольная
Первые единицы продукции будут произведены на первом заводе в силу меньших предельных издержек. При увеличении объёма выгодно будет часть продукции производить на первом заводе, а часть на втором, так как предельные издержки на первом заводе сравняются с 75. Это будет выгодно сделать при q=7,5. При наращивании объёма на втором заводе в какой-то момент выгодно будет часть продукции до произвести на первом заводе в силу более низких предельных издержек на втором участке. На графике прерывистой линией отмечен объём перехода назад на первый завод — q^*.
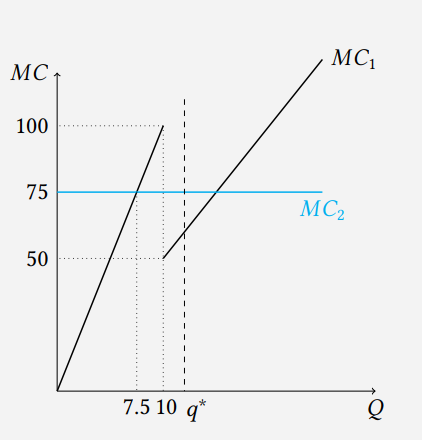
Условие перехода — превышение выгоды (зелёной площади) над дополнительными издержками (красной площадью). Красная площадь составляет (100-75)*(10-7,5)*0,5=31,25. Пусть объём перехода равен q. Тогда зеленая площадь составляет (75-5q+25)*(q-10)*0,5=0,5(q-10)(100-5q). Так как зеленая площадь растёт с ростом q на интересуемом промежутке, то для нахождения выгодной точки перехода надо приравнять площади. Решим (q − 10)(100 − 5q) = 62,5
Получим q^* = \frac{30 - 5\sqrt{2}}{2} \approx 11.46. Получаем общую функцию предельных издержек:
MC(Q) = \begin{cases} 10Q, & Q < 7.5 \\ 75, & 7.5 \leq Q \leq \frac{30 - 5\sqrt{2}}{2} \\ 5Q, & \frac{30 - 5\sqrt{2}}{2} \leq Q \leq 15 \\ 75, & Q > 15 \end{cases}
Восстановим функцию общих издержек:
TC(Q) = \begin{cases} 5Q^2, & 0 \leq Q < 7.5 \\ 75(Q - 7.5) + 5 \times 7.5^2, & 7.5 \leq Q \leq \frac{30 - 5\sqrt{2}}{2} \\ 2.5Q^2 - 2.5 \left( \frac{30 - 5\sqrt{2}}{2} \right)^2 + 75 \left( \frac{30 - 5\sqrt{2}}{2} - 7.5 \right) + 5 \times 7.5^2, & \frac{30 - 5\sqrt{2}}{2} \leq Q \leq 15 \\ 75(Q - 15) + 2.5 \cdot 15^2 - 2.5 \left( \frac{30 - 5\sqrt{2}}{2} \right)^2 + 75 \left( \frac{30 - 5\sqrt{2}}{2} - 7.5 \right) + 5 \times 7.5^2, & Q > 15 \end{cases}
Третий участок построен по следующей логике: с предельными издержками 5Q производятся единицы свыше найденного ранее количества (11.46), 2,5Q^2 это издержки, которые неслись бы, если бы все единицы производились с одинаковыми предельными издержками, затем надо вычесть 2.5 \times \left( \frac{30 - 5\sqrt{2}}{2} \right)^2 - издержки за единицы, которые на самом деле производятся по другим предельным издержкам. Затем надо прибавить издержки за всю продукцию меньше 11.46. Логика построения последнего участка аналогична.