Разъединение КПВ
В стране Z есть две области, и КПВ каждой из них в производстве апельсинов и грейпфрутов линейна. Известно, что если в стране будет производиться 20 единиц апельсинов, то оставшиеся ресурсы можно будет потратить на производство максимум 50-и единиц грейпфрутов, причем 10 из них должна будет произвести первая область. Если же в стране будет производиться 20 единиц грейпфрутов, то можно будет максимально произвести 40 единиц апельсинов, причем одна из областей должна будет произвести 30 из них. Постройте КПВ каждой из областей.
Обе КПВ линейны, значит общая КПВ имеет вид:
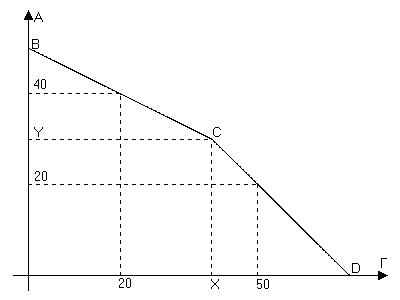
При A=20 грейпфруты производят обе области, значит точка (50;20) лежит на отрезке CD.
Аналогично, при количестве грейпфрутов, равном 20, апельсины производят также обе области, поэтому точка (20;40) должна лежать на отрезке BC.
Пусть точка полной специализации имеет координаты (X;Y).
При A=20 одна из областей производит X, а другая -50-X единиц грейпфрутов, но, как видно из графика, X>20, поэтому первая область не может производить X единиц. Значит, она производит 50-X единиц грейпфрутов, откуда делаем вывод, что X=40, и что общая КПВ «наследует» от первой области участок CD, а от второй – участок BC.
Аналогично, при количестве грейпфрутов, равном 20, одна их областей производит Y , а другая -40-Y единиц апельсинов, но из рисунка видно, что Y>20, поэтому Y=30 (а не 10).
Теперь легко определить уравнение КПВ каждой из областей (каждая из этих КПВ является отрезком прямой, на котором нам известны координаты двух точек): КПВ первой области будет задаваться уравнением A=30-G, а КПВ второй области - уравнением A=20-0.5G.
Ответ:
Первая область: A=30-G
Вторая область: A=20-0.5G.