Неравенство олигархов
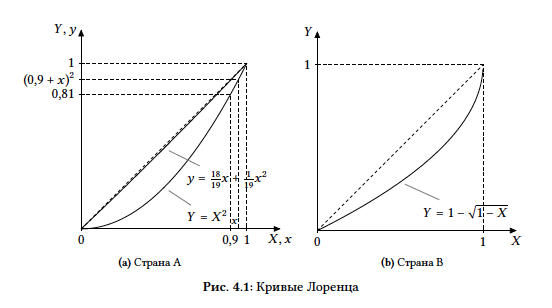
Кривая Лоренца в стране А описывается уравнением ; иными словами, доля наиболее бедного населения получает долю всего дохода общества.
- (12 баллов) Назовем 10% богатейших жителей страны олигархами. Выведите уравнение кривой Лоренца, отражающей распределение доходов среди олигархов. Иными словами, определите, какую долю y суммарного дохода всех олигархов получает доля x наиболее бедных олигархов. Что больше –– степень неравенства доходов среди олигархов или степень неравенства доходов во всей стране? (Степень неравенства будем измерять с помощью коэффициента Джини.)
- Проверьте себя: полученная вами кривая Лоренца (как и всякая кривая Лоренца) должна проходить через точки (0;0) и (1;1).
- (10 баллов) В стране B кривая Лоренца описывается уравнением . Выведите уравнение кривой Лоренца, отражающей распределение доходов среди олигархов страны B (олигархами здесь также называются 10% богатейших жителей). Что больше –– степень неравенства доходов среди олигархов страны B или степень неравенства доходов во всей стране?
- (8 баллов) Что больше – степень неравенства доходов среди 10% богатейших или среди 1% богатейших жителей страны B? Среди 1% богатейших или среди 0,1% богатейших жителей страны B?
Чтобы определить, какую долю y суммарного дохода всех олигархов получает доля x наиболее бедных олигархов, можно для каждого значения x:
-
определить, какую часть составляет доход всех олигархов общем доходе страны;
-
определить, какую часть составляет доход доли x наиболее бедных олигархов в общем доходе страны;
-
разделить второй показатель на первый.
-
90% населения, не входящие в группу олигархов, получают долю Y(0,9)=0,81 всего дохода, а олигархи, следовательно, получают 1−Y(0,9)=0,19 всего дохода.
Доля x наиболее бедных олигархов составляет долю 0,1x от всего населения страны. При этом вместе с 90% неолигархов они составляют 0,9+0,1x населения и получают всего дохода; без учета неолигархов они получают всего дохода.
Значит, в общем доходе всех олигархов доход x наиболее бедных из них составляет
Это и есть искомое уравнение кривой Лоренца.
Сравнить степень неравенства можно двумя способами.
Способ 1. (Не требует расчета коэффициентов Джини.)
Заметим, что полученная кривая Лоренца лежит ближе к линии абсолютного равенства, чем кривая Лоренца для всей страны: действительно, для , так как в этом интервале . (На Рис. 4.1a новая кривая Лоренца почти неотличима от прямой линии.) Значит, коэффициент Джини распределения доходов среди олигархов меньше, чем коэффициент Джини для всей страны. Среди олигархов степень неравенства доходов меньше, чем в стране в целом.
Способ 2. Рассчитаем коэффициенты Джини. Во всей стране коэффициент Джини равен
.
Среди олигархов коэффициент Джини равен
Поскольку , среди олигархов степень неравенства доходов меньше.
- Действуя по аналогии, получаем, что искомая кривая Лоренца будет иметь вид
Таким образом, кривая Лоренца распределения доходов среди 10% богатейших имеет точно такой же вид, как кривая Лоренца в стране в целом! Следовательно, коэффициент Джини распределения доходов среди олигархов точно такой же, как в стране в целом.
Примечание. Для ответа на вопрос не понадобилось рассчитывать сам коэффициент Джини (он равен 1/3).
- Представим себе страну C, населенную только олигархами страны B. 1% богатейших жителей страны B являются 10% богатейших жителей страны C (то есть олигархами среди олигархов). Таким образом, нам нужно сравнить неравенство доходов в стране С в целом и неравенство доходов среди олигархов страны C.
В пункте 2 мы решили точно такую же задачу для страны B; при этом мы вывели, что в стране C кривая Лоренца имеет точно такой же вид как в стране B. Значит, и ответ будет таким же: кривая Лоренца среди олигархов страны C будет иметь такой же вид, как в стране С в целом, и коэффициент Джини будет тем же самым. Продолжая по аналогии, получаем, что и среди 0,1% богатейших жителей страны B (1% богатейших жителей страны C) коэффициент Джини будет точно таким же.
Примечание:
Распределение доходов в богатейших слоях общества в реальном мире скорее похоже на распределение доходов в стране B, чем в А. Во многих странах распределение доходов среди 5-10% богатейших жителей хорошо описывается кривой Лоренца . Для страны B , а, например, в настоящее время в США . Такое распределение называется распределением Парето в честь итальянского экономиста Вильфредо Парето, который первым обнаружил такую форму распределения доходов более 100 лет назад. Свойство, полученное нами в п.2 и п.3 (кривая Лоренца для t% богатейших одинакова для любого t) выполняется для любого ; этот феномен имеет место и в реальном мире среди обеспеченных слоев населения.
См. также: Фрактал