Неравенство: внутри и между
Экономисты интересуются вопросом неравенства доходов не только внутри одной страны, но и между странами. В 2024 г. Нобелевская премия по экономике как раз была присуждена за исследование причин неравенства между странами. Исследования показывают, что за последние 45 лет неравенство доходов внутри стран в среднем увеличилось, но неравенство между странами снизилось.
Представим себе две страны (первую и вторую), в которых есть по две группы населения, в каждой из которых доход распределен равномерно. Обозначим за x_i долю более бедной группы в населении страны i, за a_i — среднедушевой доход бедных в стране i, за b_i — среднедушевой доход богатых в стране i (b_i\geq a_i\geq 0, причем суммарный доход каждой страны положителен). Численность населения в двух странах одинакова.
Определим средний внутри страновой коэффициент Джини G_{внутри} как среднее арифметическое коэффициентов Джини в двух странах. Определим межстрановой коэффициент Джини G_{между} как коэффициент Джини, отражающий неравенство доходов в гипотетическом мире, в котором есть две страны с таким же населением и суммарным доходом в каждой из стран, но в котором доход внутри стран распределен равномерно. Наконец, пусть G_{мира} — коэффициент Джини, отражающий полное неравенство доходов между всеми жителями двух стран.
а) ( 4 балла) Найдите G_{внутри}, \ G_{между} и G_{мира}, если x_1=x_2=0,5, a_1=10, b_1=40a_2=20, b_2=130.
Пусть N — население каждой из стран.
Рассчитаем y_1 и y_2 — доли доходов бедных в суммарном доходе каждой из стран.
y_1=\frac{10\cdot 0.5N}{10\cdot 0.5N+40\cdot 0.5N}=\frac{5N}{25N}=0.2, \qquad y_2=\frac{20\cdot 0.5N}{20\cdot 0.5N+130\cdot 0.5N}=\frac{10N}{75N}=\frac{2}{15}.
Значит, коэффициенты Джини в двух странах равны G_1=x_1-y_1=0,5-0,2=0,3, G_2=x_2-y_2=0,5-2/15=11/30.
Следовательно, средний внутристрановой коэффициент Джини равен
G_{\text{внутри}}=\frac{G_1+G_2}{2} =\frac{\tfrac{3}{10}+\tfrac{11}{30}}{2} =\frac{\tfrac{9}{30}+\tfrac{11}{30}}{2} =\frac{\tfrac{20}{30}}{2} =\frac{1}{3}.
Среднедушевой доход ниже в стране 1, чем в стране 2 (0,5*10+0,5*40<0,5*20+0,5*130 ), значит, страна 1 — более бедная «группа населения» в мире
Доля страны 1 в мировом доходе составляет \frac{10\cdot 0.5N + 40\cdot 0.5N} {10\cdot 0.5N + 40\cdot 0.5N + 20\cdot 0.5N + 130\cdot 0.5N} = \frac{50}{50+150} = 0.25..
Ее доля в мировом населении равна 0,5. Значит, межстрановой коэффициент Джини равен G_{между}=0,5-0,25=0,25 .
Наконец, чтобы посчитать мировой коэффициент Джини, построим мировую кривую Лоренца. Она представляет из себя ломаную линию, соединяющую точки(0;0), \ (0,25;0,05), \ (0,5;0,15), \ (0,75;0,35), \ (1;1).
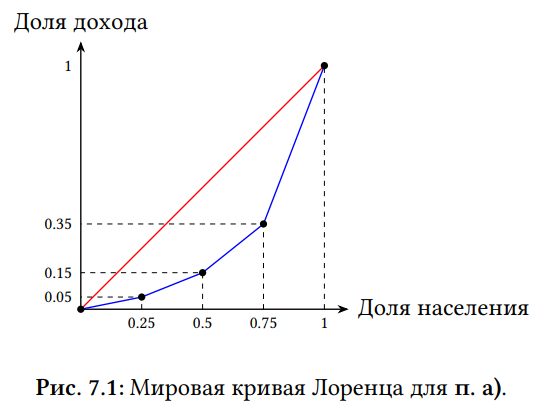
Отсюда находим, что площадь под ней равна S=0,2625, а общемировой коэффициент Джини равен G_{мира}=\frac{1/2-S }{1/2}=1-2S=0,475.
Ответ: G_{внутри }=1/3, G_{между}=1/4 , G_{мира}=0,475 .
б) ( 8 баллов) Теперь допустим, что x_1=x_2=0,8. Значения среднедушевых доходов a_i, \ b_i неизвестны. Найдите максимально возможное и минимально возможное значения G_{мира}, если G_{внутри}=0,2 , G_{между}=0,3 .
Определим, как взаимно расположены среднедушевые доходы a_1, \ a_2, \ b_1, \ b_2.
Пусть Y_i — суммарный доход страны i. Не нарушая общности, можно считать, что Y_1\leq Y_2.
Тогда G_{\text{между}}=0{,}5-\frac{Y_1}{Y_1+Y_2}=0{,}3, откуда Y_2/Y_1=4.
Пусть y_i — доля дохода бедных в каждой стране в ее общем доходе.
Тогда G_{\text{внутри}}=\tfrac{1}{2}\,(x_1-y_1+x_2-y_2) =\tfrac{1}{2}\,(1{,}6-y_1-y_2)=0{,}2, откуда y_1+y_2=1,2.
Имеем b_1=\frac{(1-y_1)Y_1}{(1-x_1)N},\qquad a_2=\frac{y_2Y_2}{x_2^2N}. Покажем, что из имеющихся данных следует, что b_1<a_2.
Действительно, \begin{aligned} b_1<a_2 &\iff \frac{(1-y_1)Y_1}{(1-x_1)N}<\frac{y_2Y_2}{x_2^2N} \iff 1-y_1<\frac{y_2Y_2}{Y_1}\cdot\frac{1-x_1}{x_2}\iff 1-y_1<y_2\cdot 4\cdot\frac{0.2}{0.8} \iff y_1+y_2>1. \end{aligned}
но последнее верно в силу y_1+y_2=1,2. Значит, b_1<a_2, откуда a_1\leq b_1<a_2\leq b_2.
Отсюда получаем, что кривая Лоренца мира соединяет точки (0;0), \ (0,4;0,2y_1), \ (0,5;0,2), \ (0,9;0,2+0,8y_2), \ (1;1).
Удвоенная площадь под ней равна 2S=0,1y_1+0,4y_2+0,3, а коэффициент Джини G_{мира }=1-2S=0,7-0,1y_1-0,4y_2. Нам нужно максимизировать и минимизировать значение выражения 0,7-0,1y_1-0,4y_2 при ограничениях y_i\geq 0, \ y_i\leq 0,8 (из-за неотрицательности коэффициентов Джини в двух странах), и y_1+y_2=1,2. Выражаем y_2=1,2-y_1, откуда G_{мира }=0,7-0,1y_1-0,4(1,2-y_1)=0,22+0,3y_1.
y_1 принимает значения от 0,4 (в силу y_2=1,2-y_1\leq 0,8 ) до 0,8. Для минимизации G_{мира} нужно взять y_1=0,4, для максимизации y_1=0,8.
Значит, min G_{\text{мира}}=0.22+0.3\cdot 0.4=0.34, \qquad \max G_{\text{мира}}=0.22+0.3\cdot 0.8=0.46.
Ответ: минимальное значение G_{мира} равно 0,34, максимальное — 0,46.