Dynamic Equilibrium
Oil (good A) and Gas (good B) are substitutes in consumption; the demand and supply functions are given by:
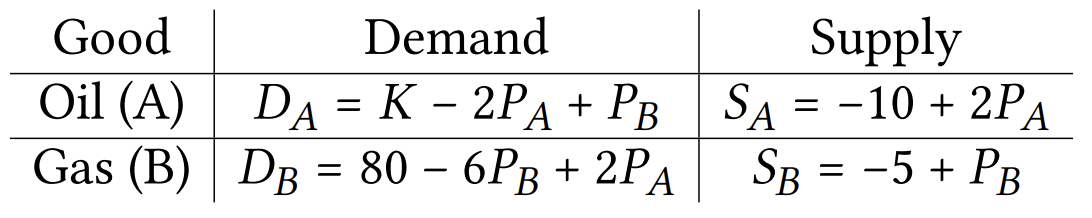
(a) (5 rp) Find equilibrium prices P^*_A and P^*_B if K=210.
By setting demand equal to supply on both markets, we get a system of two equations:
\begin{cases} 210 - 2P_A + P_B = -10 + 2P_A, \\ 80 - 6P_B + 2P_A = -5 + P_B. \end{cases}
From that we get P^*_A = 62.5 and P^*_B=30
(b) (10 rp) Now consider a dynamic version of this model. We consider the demand for Gas constant for simplicity, but the demand for Oil is volatile. In period t, parameter K takes the value of Kt. Suppose that K1=210, so in the first period, the equilibrium from part (a) realizes.
For producers of both natural resources, it takes some time to change production capacity, so they have to make a production decision one period before the actual sale occurs. In the first period (t=1), they expect the demand for Oil to fall sharply, so the expected K2 equals 80. How many units of Oil and Gas will be produced for selling in period 2?
The producers predict future prices thinking that K=80, that is, solving the system:
\begin{cases} 80 - 2P_A + P_B = -10 + 2P_A, \\ 80 - 6P_B + 2P_A = -5 + P_B. \end{cases}
From that we get P_A=27.5 and P_B=20. Plugging these to the equations, we get the outputs: Q_A=45, Q_B=15. These outputs will actually be produced for sale in period 2.
(c) (5 rp) The prediction of demand decline turned out to be wrong, so K2 remained at level 210. Still, the goods are produced, and capacity is exhausted. What prices of Oil and Gas will clear the market?
Given that the outputs are already produced, when t=2 comes, supply is perfectly inelastic: S_A=45, S_B=15. The actual demand function has K=210. The markets are cleared when:
\begin{cases} 210 - 2P_A + P_B = 45, \\ 80 - 6P_B + 2P_A = 15. \end{cases}
Of course, the prices skyrocketed: P_A=105.5 and P_B=46.
(d) (10 rp) Suppose that starting from period 2, firms' expectations are naive. This means that they always expect the next period's prices to equal the prices in the current period and make decisions about future production based on this prediction. At the same time, the actual value of K always remains 210. What will happen to prices and outputs when t \rightarrow \infty?
We can continue this process further. At prices P_A=105.5 and P_B=46, the firms will produce Q_A=201, Q_B=41. This, in turn, will lead to market-clearing prices P_A=9.3 and P_B=9.6. At these prices, the firms will produce Q_A=8.6, Q_B=4.6. This will lead to prices at around 128 and 55. It can be seen that the system diverges — prices fluctuate more and more. At some point, prices and/or outputs will reach zero levels, and if the firms' expectations remain naive, the system will go through a cycle of extremely high and extremely low outputs and prices.