Задача 1.2.5. Тарифище
Для производства продукции фирма покупает электричество и труд. Труд фирма нанимает на конкурентном рынке, зарплата на котором установилась на уровне w=2. Электричество фирма нанимает у электростанции по следующему тарифу:
- Для первых 32/3 единиц электричества цена составляет 8 за единицу;
- Цена всех последующих единиц электричества (сверх 32/3 ) составляет 2 за единицу.
Производственная функция фирмы имеет следующий вид: Q(E, \ L)=\sqrt [4] {EL}, где E — количество электричества, L — количество труда.
а) Запишите функцию затрат на электричество от количества используемого электричества c(E).
\\ Олимпиада ЭШФЭН, 2023
c(E) = \begin{cases} 8E, & E \leq \frac{32}{3} \\ 2\left(E - \frac{32}{3}\right) + 8 \cdot \frac{32}{3} = 2E + 64, & E > \frac{32}{3} \end{cases}
б) Выведите функцию издержек фирмы TC(Q). На графике изобразите функцию предельных издержек фирмы MC(Q).
TC = 2L + c(E) = \begin{cases} 2L + 8E, & E \leq \frac{32}{3} \\ 2L + 2E + 64, & E > \frac{32}{3} \end{cases}
TC = \begin{cases} \frac{2Q^4}{E} + 8E, & E \leq \frac{32}{3} \\ \frac{2Q^4}{E} + 2E + 64, & E > \frac{32}{3} \end{cases}
Проминимизируем оба выражения по E, применяя неравенство Коши (можно так же минимизировать, используя производную). Проверим области определения позднее.
\frac{2Q^4}{E} + 8E = 2 \sqrt{\frac{2Q^4}{E} \cdot 8E} = 8Q^2 \Leftrightarrow \frac{2Q^4}{E} = 8E \Leftrightarrow E = \frac{Q^2}{2}
\frac{2Q^4}{E} + 2E + 64 = 2 \sqrt{4Q^4} = 4Q^2 + 64 \Leftrightarrow E = Q^2
Приведём минимизацию только для одной части функции, так как они имеют одинаковую форму.
C = \frac{2Q^4}{E} + 8E, \quad C_E' = 8 - \frac{2Q^4}{E^2} = 0 \Rightarrow E = \frac{Q^2}{2}, \quad C_E''\left(\frac{Q^2}{2}\right) > 0
Найдем, при каких значениях Q выгоднее использовать первый участок:
8Q^2 < 4Q^2 + 64
Q^2 < 16 \\ Q < 4
То есть до Q=4 выгоднее использовать E\leq 32/3, а после выгоднее использовать большие значения количества электричества, при этом условия оптимума выполняются, так как \frac{4^2}{2} < \frac{32}{3}, \quad 4^2 > \frac{32}{3}
Итого функция издержек выглядит следующим образом:
TC(Q) = \begin{cases} 8Q^2, & Q \leq 4 \\ 4Q^2 + 64, & Q > 4 \end{cases}
График предельных издержек выглядит следующим образом:
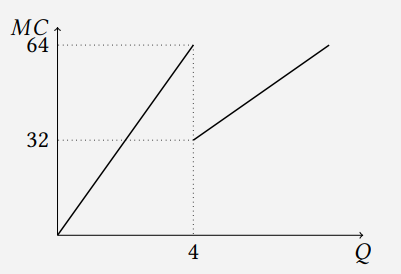
Ключевые точки:(4, \ 64), \ (4, \ 32).
в) У фирмы появилась возможность производить товары на новом заводе, средние издержки на котором постоянны и равны 50. Выведите новую функцию издержек фирмы.
Функция издержек на втором заводе имеет вид TC_2=50Q_2. Общие издержки равны:
TC = \begin{cases} 50Q_2 + 8Q_1^2, & Q_1 \leq 4 \\ 50Q_2 + 4Q_1^2 + 64, & Q_1 > 4 \end{cases}
Отдельно прооптимизируем каждый участок, то есть найдём оптимальное распределение между первым и вторым заводом при условии Q_1+Q_2=Q, а затем при каждом значении Q выберем подходящий участок. Начнём с первого участка:
TC_{\leq 4} = 50Q - 50Q_1 + 8Q_1^2 \to \min_{Q_1 = Q - Q_2 \leq 4}
Это парабола ветвями вверх, минимум в вершине: Q_1=50/16=3,125<4. Но если Q<3,125, то берём граничную точку — Q_1=Q, так как при движении к вершине значение функции уменьшается. Выходит:
TC_{\leq 4} = \begin{cases} 8Q^2, & Q \leq 3.125 \\ 3.125^2 \cdot 8 - 50 \cdot 3.125 + 50Q = 50Q - 78.125, & Q > 3.125 \end{cases}
Второй участок:
TC_{> 4} = 50Q - 50Q_1 + 4Q_1^2 + 64 \to \min_{Q_1 = Q - Q_2 > 4}
Это парабола ветвями вверх, максимум в вершине: Q_1=50/8=6,25>4. Если 4<Q<6,25, то Q_1=Q. Выходит:
TC_{> 4} = \begin{cases} 4Q^2 + 64, & Q \in (4, 6.25] \\ 50Q - 50 \cdot 6.25 - 4 \cdot 6.25^2 + 64 = -92.25 + 50Q, & Q > 6.25 \end{cases}
Теперь при каждом значении Q выберем оптимальный участок. При Q\leq 4 есть только
по одному кандидату (TC\leq 4). При Q>4 давайте сравним второй участок TC\leq 4 первый участок TC>4. Если окажется так, что при каком-то подходящем значении первый участок становится выгоднее второго участка TC\leq 4, то решение окончено, ведь для значений более 6,25 TC>4 явно выгоднее:
4Q^2 + 64 < 50Q - 78.125
4Q^2 - 50Q + 142.125 < 0
Получаем корни Q = \frac{50 + \sqrt{226}}{8} \approx 4.37, \quad 8.13 (обычно на олимпиадах не допускается округление). Выходит, что для 4<Q<4,37 выгодно использовать TC\leq 4, а при Q\geq 4,37 выгоднее использовать TC>4. Запишем итоговый ответ:
TC = \begin{cases} 8Q^2, & Q \leq 3.125 \\ 50Q - 78.125, & 3.125 < Q < 4.37 \\ 4Q^2 + 64, & 4.37 \leq Q \leq 6.25 \\ 50Q - 92.25, & Q > 6.25 \end{cases}
Допускаются нестрогие знаки на обоих пересекающихся участках.