Теория фирмы. Задача 24
Для каждого пункта найдите условия оптимума, то есть соотношения между величинами, которые должны выполняться в оптимуме (в том числе и если количества товаров равны 0 ), при выводе общей функции издержек TC=f(Q), при a>0, \ b>0, \ c>0. В явном виде функцию выводить не требуется. Также нарисуйте на графике функции Q_1(Q), \ Q_2(Q) и Q_3(Q), то есть то, как примерно будет меняться распределение производимого товара по заводам. Если в задаче возможны несколько вариантов ответа в зависимости от параметров, укажите их все.
а) TC_1 = aQ_1^2, \quad TC_2 = b\sqrt{Q_2}
Сначала Q_1=Q, Q_2=0, потом MC_1=MC_2.
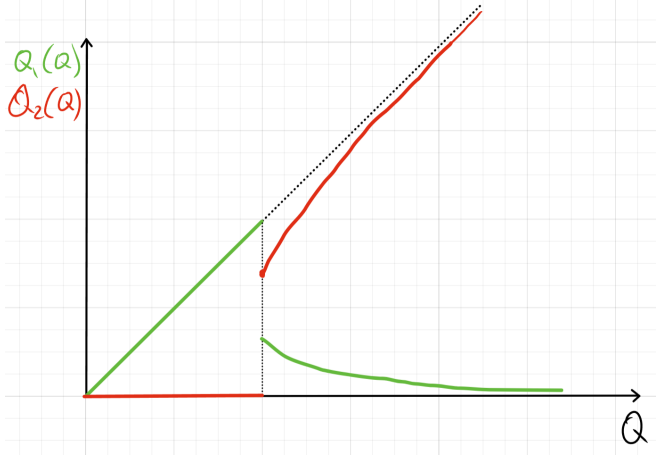
б) TC_1 = a\sqrt{Q_1}, \quad TC_2 = b\sqrt{Q_2}
При a>b производим только на 2 заводе, а при a<b только на первом (при a=b безразлично на каком). На графике первый вариант:
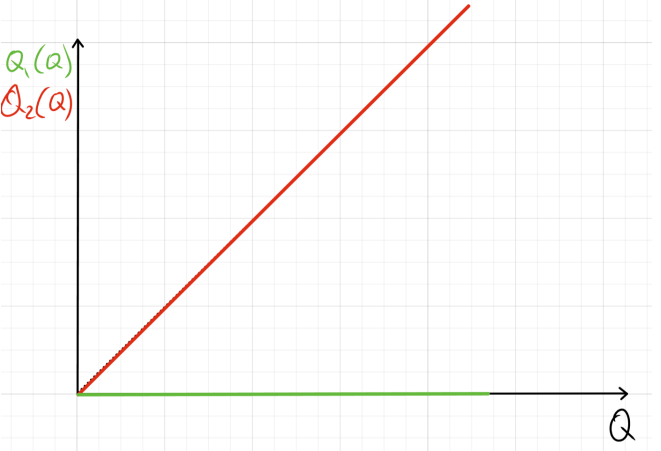
в) TC_1 = aQ_1^2 + cQ_1, \quad TC_2 = bQ_2^2
Сначала производим только на первом заводе, а затем MC_1=MC_2, то есть:
TC = \begin{cases} bQ^2, & Q \leq \frac{c}{2b} \\ \frac{ab}{a+b}Q^2 + \frac{bc}{a+b}Q - \frac{c^2}{4a+4b}, & \frac{c}{2b} < Q \end{cases}
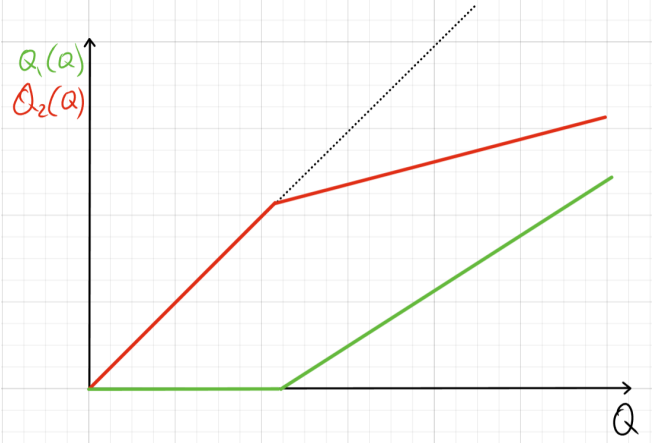
г) TC_1 = aQ_1^2 + cQ_1, \quad TC_2 = b\sqrt Q_2
При низких c сначала производим только на первом заводе, а затем MC_1=MC_2, и после все только на втором. При высоких c сначала производим только на первом заводе, а затем сразу только на втором. Оба варианта графиков, соответственно:
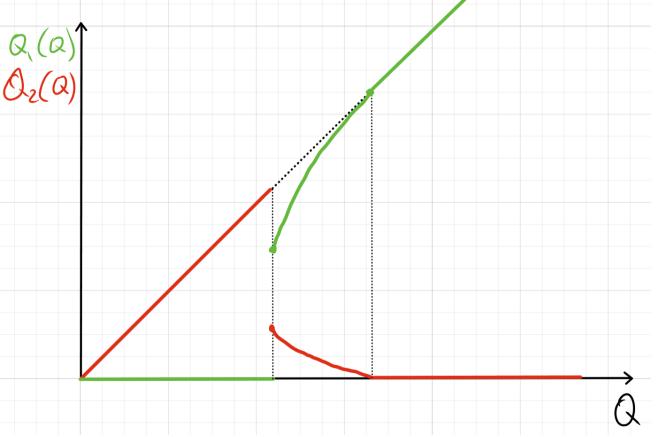
\\
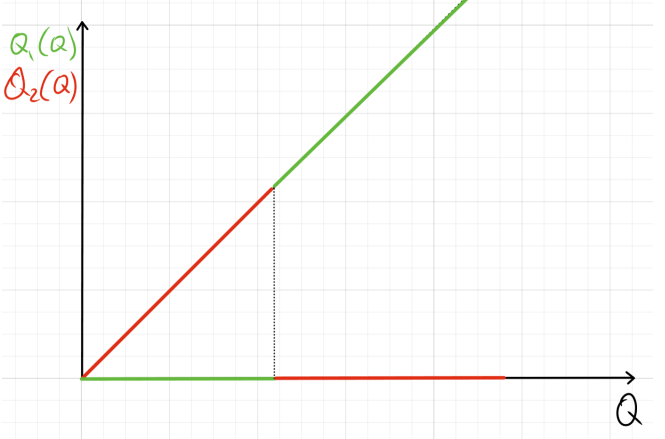
д) TC_1 = aQ_1, \quad TC_2 = bQ_2
Все на первом заводе при a<b и все на втором заводе при b>a. Второй вариант на графике:
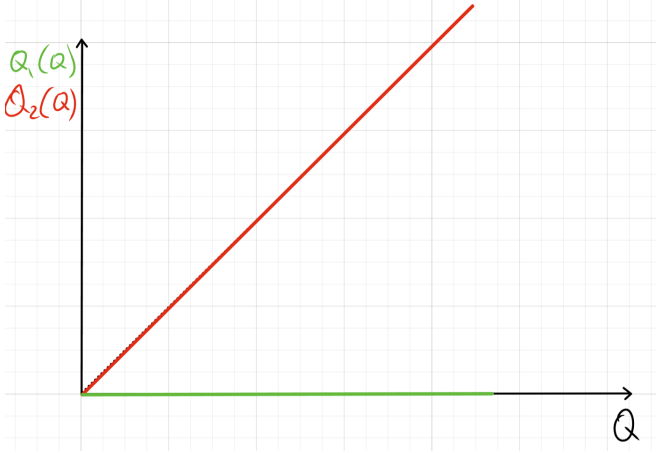
е) TC_1 = aQ_1^2+cQ_1, \quad TC_2 = bQ_2
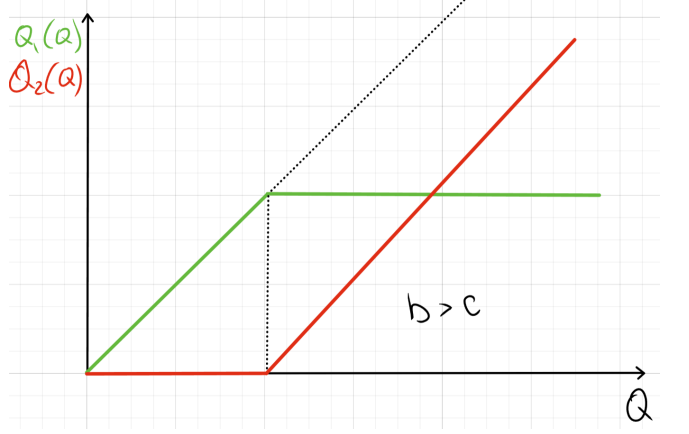
При b<c все производим только на втором заводе, при b>c сначала на первом, потом на втором так, что MC_1=MC_2. Издержки для второго варианта:
TC = \begin{cases} aQ^2 + cQ, & Q \leq \frac{b}{2a} \\ bQ - \frac{b^2 - 2bc}{4a}, & \frac{b}{2a} < Q \end{cases}
Графики обоих вариантов:
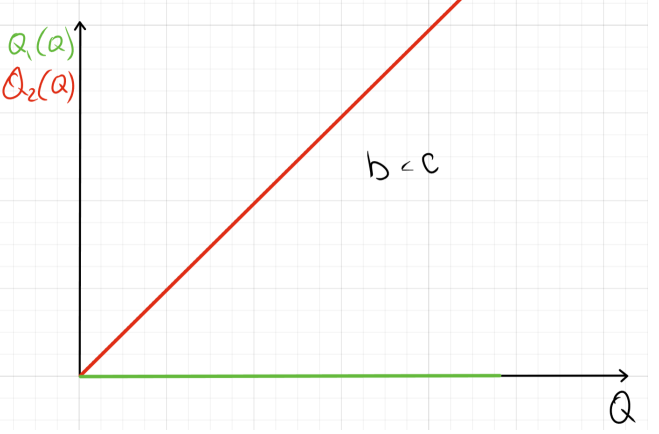
\\ 
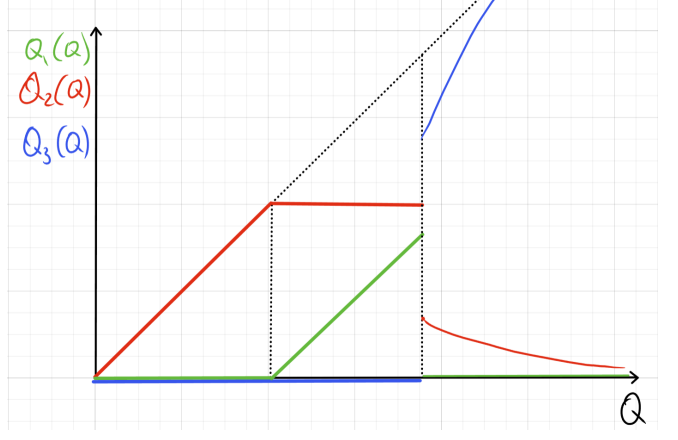
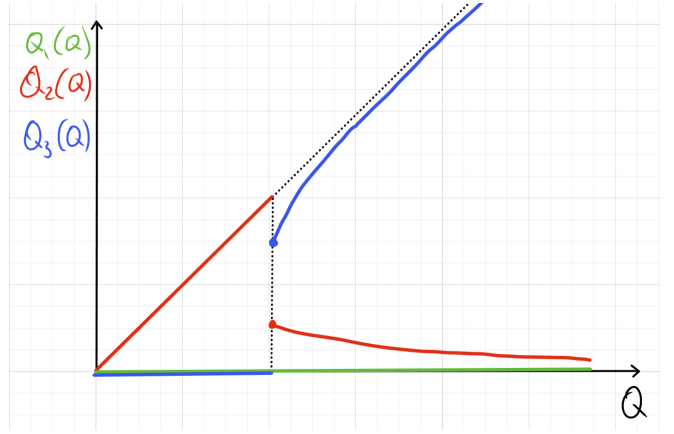
ж) TC_1 = aQ_1, \quad TC_2 = bQ_2^2, \quad TC_3 = c\sqrt{Q_3}
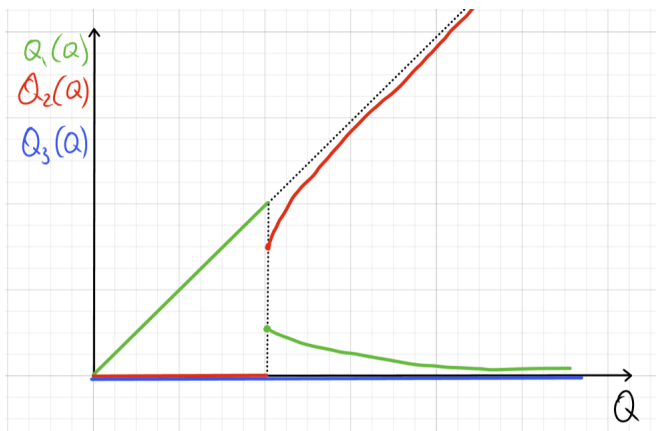
При высоких c cначала производим все на втором заводе, затем на первом при условии MC_1=MC_2, а затем на втором и третьем при условии MC_2=MC_3 и Q_1=0. При низких c cначала производим все на втором заводе, а затем на втором и третьем при условии MC_2=MC_3 и Q_1=0. Оба варианта, соответственно, на графиках:
\\ 
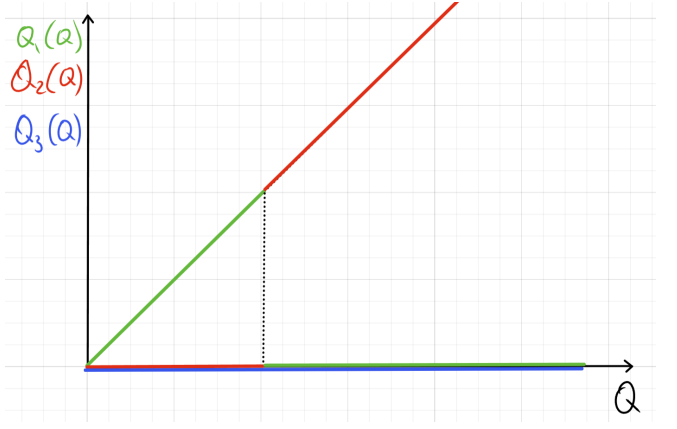
з) TC_1 = aQ_1, \quad TC_2 = b\sqrt{Q_2}, \quad TC_3 = c\sqrt{Q_3}
Производим все только на одном заводе. Среди второго и третьего никогда не используем завод с более высоким коэффициентом. Сначала используем первый завод, а затем другой. Пример для b<c :
и) TC_1 = aQ_1^2, \quad TC_2 = b\sqrt{Q_2}, \quad TC_3 = c\sqrt{Q_3}
Среди второго и третьего никогда не используем завод с более высоким коэффициентом. Например, для b<c сначала Q_1=Q, \ Q_2=0, потом MC_1=MC_2 :