Блиц
В первом задании олимпиады вам предстоит решить три не связанных друг с другом коротких задачи.
а) ( 4 балла)В январе 2025 года китайская компания DeepSeek представила чат-бота на основе собственной большой языковой модели. По заявлению компании, новая технология обучения модели потребовала в несколько раз меньше вычислительных ресурсов, чем у конкурентов. Это вызвало ожидания снижения спроса на графические процессоры, и акции NVIDIA –– крупнейшего их производителя –– резко упали.
Рассмотрим фирму «Джевонс и Ко», использующую чипы NVIDIA для производства нейросетевых решений. Чтобы выпустить q единиц продукта, фирма использует x чипов, производственная функция q=a\sqrt x, где a>0 0. Рыночная цена продукта составляет 2 д.е. за единицу, один чип стоит 1 д.е. Распространение новой технологии повышает параметр a с 2 до 5. Рассчитайте, как изменится количество закупаемых фирмой чипов, и содержательно объясните направление этого изменения.
Прибыль фирмы составляет
\pi(x)=pq-cx=2a\sqrt x-x.
Это квадратичная функция (парабола ветвями вниз) от \sqrt x, следовательно, максимум достигается при \sqrt x=a, откуда x=a^2.
Таким образом, спрос «Джевонс и Ко» на чипы до появления DeepSeek (при a=2 )
был равен 4, а после появления DeepSeek (a=5 ) увеличился до 25.
Объяснение. В результате появления DeepSeek MRP_x (предельная отдача от использования чипов в денежном выражении) увеличилась: каждый следующий чип стал приносить больше выпуска, т.е. больше выручки при тех же ценах. Поскольку затраты на чипы не изменились, выгодно расширить производство, пока использование дополнительных чипов не перестанет окупаться.
Таким образом, несмотря на повышение эффективности использования ресурса, его потребление выросло. Этот эффект известен в экономике как парадокс Джевонса (например, технология, экономящая топливо, ведёт к повышению его суммарного расхода).
б) ( 4 балла) Из города А в город Б идут две дороги: старая и новая, проезд по ним бесплатный. Если по старой дороге едут x машин в час, то время в пути между городами составляет 40+x/20 минут. Если по новой дороге едут y машин в час, то время в пути между городами составляет 30+y/30 минут. Суммарный поток по двум дорогам составляет 1000 машин в час. Каждый водитель выбирает дорогу так, чтобы минимизировать сумму денежной ценности своего времени в пути (минуту своего времени он ценит в 10 рублей) и платы за проезд (если она есть). Время в пути водитель узнаёт через навигатор, использующий текущие данные загруженности дорог; небольшой собственный вклад в загруженность дороги никто не учитывает. В министерстве транспорта заметили, что новая дорога слишком загружена, и решили сделать ее платной. Какую плату p за проезд по новой дороге следует установить, чтобы минимизировать суммарное время в пути всех водителей на двух дорогах?
Пусть транспортные потоки распределились так: y машин в час едут по новой дороге, а 1000-y машин в час — по старой дороге. Если плата за пользование новой дорогой составляет p, то суммарные денежно-временные затраты водителя, выраженные в рублях, составляют 400+\frac{1000-y}{2}, если он едет по старой дороге, и 300+y/3+p, если он едет по новой дороге. Водитель поедет по новой дороге, если 300+y/3+p<400+\frac{1000-y}{2}, т.е. если y<720-\frac{6}{5}p, и по старой, если y>720-\frac{6}{5}p.
Если y<720\frac{6}{5}p, то водители, выезжающие на развилку между новой и старой дорогой, выберут новую дорогу, так что поток y по ней будет расти, пока не станет равен 720-\frac{6}{5}p, и до этого же значения он будет падать, если y>720-\frac{6}{5}p. Следовательно, спрос на пользование новой дорогой при стоимости проезда p составляет y(t)=720-\frac{6}{5}p.
При потоке y по новой дороге суммарные потери времени всех водителей составляют
(1000-y)(40+\frac{1000-y}{20})+y(30+\frac{y}{30})=\frac{5}{60}y^2+110y+90000.
Это квадратичная функция (парабола ветвями вверх), достигающая минимума по y при y=660.
Следует установить такую стоимость проезда p, чтобы достичь оптимальной загрузки новой дороги y(p)=720-\frac{6}{5}t=660. Отсюда оптимальная стоимость проезда p составляет 50 рублей.
в) ( 4 балла) В деревне есть 60 крестьянских хозяйств, каждое из которых располагает 1 единицей земли и 5 единицами рабочего времени. Жители деревни умеют выращивать пшеницу и лён, а также выпекать хлеб и изготавливать ткань. Производство единицы пшеницы требует 5 единиц рабочего времени и 1 единицы земли, а производство единицы льна требует только 1 единицы земли и не требует труда. Производство единицы хлеба требует 1 единицы пшеницы и 1 единицы рабочего времени. Производство единицы ткани требует единицы льна и 4 единиц рабочего времени. Опишите формулой вида y=f(x) (где x –– хлеб, y –– ткань), как устроена КПВ этой экономики.
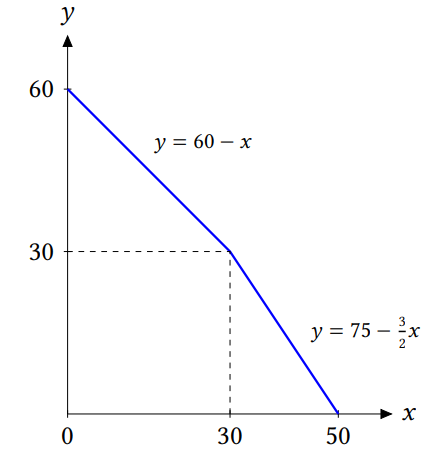
Пусть в деревне произведено x единиц хлеба. Это означает, что произведено не менее x единиц пшеницы и на производство хлеба затрачено не менее x единиц рабочего времени. На всю производственную цепочку, дающую на выходе хлеб, затрачено не менее x единиц земли и не менее 6x единиц рабочего времени. Следовательно, на производственную цепочку, дающую на выходе ткань, остаётся не более 60-x единиц земли и не более 300-6x единиц рабочего времени. Из такого количества ресурсов можно произвести не более 60-x единиц льна, т.е. не более min\{60-x, 75-\frac{3}{2}x\} единиц ткани. Этот объём производства ткани достижим, так как в предыдущих рассуждениях, где нужно, можно заменить «не менее» и «не более» на «ровно». Хлеба не может быть произведено больше 50 единиц, а ткани –– больше 60 единиц.
Ответ: y=min\{60-x, 75-\frac{3}{2}x\}, 0\leq x\leq 50.