Инвестиции в образование
Повышение уровня образования является одним из инструментов, с помощью которых государство может стимулировать экономический рост, повышать уровень жизни населения и снижать социальное неравенство. Инвестиции в образование способствуют формированию квалифицированной рабочей силы, повышают производительность труда и способствуют развитию инновационных отраслей. Поэтому правительства многих стран рассматривают финансирование образования не как расход, а как стратегическую инвестицию в будущее общества и экономики. В этой задаче мы рассмотрим модель выбора образовательной траектории и последствия вмешательства в него государства.
Предположим, что в некоторой стране ежегодно выпускается 140 тысяч школьников. Все выпускники различаются по уровню полученного школьного образования, который обозначим как \theta , где \theta принимает значения от 0 до 1. Распределение выпускников по уровню школьного образования равномерное. Например, доля выпускников с уровнем образования в диапазоне от \theta = 0.2 до \theta = 0.5 составляет 0.5-0.2=0.3, а их численность равна 0.3*140=52 тысячи человек. Выпускниками с точно заданными значениями (например, ровно \theta = 0.2 или \theta = 0.5 ) можно пренебречь.
В стране существует два университета: престижный и менее престижный. Престижный университет обеспечивает качество образования s_1=2, а менее престижный — s_2=1. Стоимость обучения в престижном университете равна p_1, а в менее престижном — p_2. Оба университета максимизируют свою прибыль, устанавливая цены на обучение независимо и одновременно, при этом издержки на обучение отсутствуют. Каждый выпускник выбирает один из трёх вариантов:
- обучаться в престижном университете,
- обучаться в менее престижном университете,
- не продолжать обучение вовсе.
Если выпускник с уровнем школьного образования \theta решает поступить в университет, то его полезность определяется формулой: U=s_i*\theta-p_i, где s_i и p_i, соответствуют выбранному университету. Такая полезность объясняется тем, что выпускники с более высоким уровнем образования получают большую отдачу от высшего образования. Если выпускник не продолжает обучение, его полезность равна нулю. Каждый выпускник стремится максимизировать свою полезность.
a) ( 15 баллов) Найдите равновесные цены на высшее образование, которые установят университеты. То есть определите такие значения p_1 и p_2, при которых ни один из университетов не захочет изменить свою цену, если цена другого университета остается неизменной.
1. Определение пороговых значений
Пусть выпускник с уровнем образования \theta выбирает между университетами, максимизируя полезность:
U_1=s_1*\theta-p_1, \quad U_2=s_2*\theta-p_2
Найдём абитуриента, которому безразлично какое образование получать (\hat{\theta}) :
s_1 \hat{\theta} - p_1 = s_2 \hat{\theta} - p_2
\hat{\theta} (s_1 - s_2) = p_1 - p_2
\hat{\theta} = \frac{p_1 - p_2}{s_1 - s_2}
s1 − s2
Минимальное значение \theta_{\min}, при котором выпускник решает учиться в менее престижном университете, находится из условия:
s_2 \theta_{\min} - p_2 = 0
\theta_{\min} = \frac{p_2}{s_2}
2. Определение спроса на университеты
Число студентов в каждом университете:
N_1 = 140 (1 - \hat{\theta}), \quad N_2 = 140 (\hat{\theta} - \theta_{\min})
3. Вывод функций реакции университетов
Прибыль университетов:
\Pi_1 = p_1 \cdot N_1 = p_1 \cdot 140(1-\theta), \qquad \Pi_2 = p_2 \cdot N_2 = p_2 \cdot 140(\theta-\theta_{\min})
Подставляем выражения для \theta и \theta_{\min} :
\Pi_1 = p_1 \cdot 140\!\left(1-\frac{p_1-p_2}{\,s_1-s_2\,}\right), \qquad \Pi_2 = p_2 \cdot 140\!\left(\frac{p_1-p_2}{\,s_1-s_2\,}-\frac{p_2}{s_2}\right)
Максимизируем по p_1 и p_2, получаем линии реакции:
\begin{cases} \displaystyle p_1=\dfrac{p_2+(s_1-s_2)}{2},\\[8pt] \displaystyle p_2=\dfrac{s_2}{2s_1}\,p_1 \end{cases} \quad\Longrightarrow\quad \begin{cases} \displaystyle p_1=\dfrac{p_2+1}{2},\\[8pt] \displaystyle p_2=\dfrac{p_1}{4} \end{cases}
Решая систему уравнений, получаем равновесные цены:
p_1^{*}=\frac{4}{7},\qquad p_2^{*}=\frac{1}{7}
Пороговые значения:
\theta_{\min}=\frac{1}{7},\qquad \theta=\frac{3}{7}
Примечание:
В решении выше не рассмотрены «крайние случаи», когда при выбранных на линии реакции p_1 и p_2 значение каких-то из \theta не попадает в область определения. Заметим, что во всех таких случаях не достигается равновесие.
1. Допустим, \hat{\theta}=\frac{p_{1}-p_{2}}{\,s_{1}-s_{2}\,}>1, тогда прибыль первого университета равна нулю и если прибыль второго больше нуля, то первый хочет отклониться и понизить цену, иначе – отклониться желает второй.
2. Допустим, что \theta_{\min}>\hat{\theta}\quad \text{или}\quad \theta_{\min}>\frac{p_{1}}{s_{1}}, то есть минимального значения при котором абитуриенту безразлично поступать ли во второй университет. В этом случае прибыль второго университета равна нулю и он хочет отклониться, понизив цену. Понизить цену он может, так как s-2/p_2>0.
3. \theta_{\min} не может быть меньше нуля. Тогда мы имеем, что: 0 < \theta_{\min} < \hat{\theta} < 1 в равновесии.
Иллюстрация:
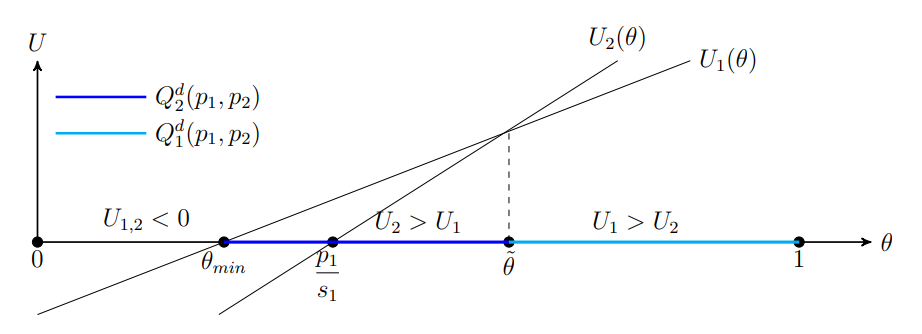
Ответ: p_1^*=4/7 \quad p_2^*=1/7
б) ( 5 баллов) Государство обеспокоено числом выпускников, не получающих высшее образование, и решает инвестировать в повышение качества. Теперь качество обучения в престижном университете увеличивается до s_1=3, а в менее престижном — до s_2=2. Определите, насколько увеличится число выпускников, поступающих в университеты, по сравнению с пунктом a).
Так как в пункте a) мы уже решили задачу оптимизации в общем виде, подставим новые значения s :
\begin{cases} p_1=\dfrac{p_2 + (s_1-s_2)}{2},\\[4pt] p_2=\dfrac{s_2}{2s_1}\,p_1 \end{cases} \;\Rightarrow\; \begin{cases} p_1=\dfrac{p_2+1}{2},\\[4pt] p_2=\dfrac{p_1}{3} \end{cases} \;\Rightarrow\; p_1=\dfrac{3}{5},\quad p_2=\dfrac{1}{5}.
Для пункта a) количество выпускников, которое не получило образование: N\,\theta_{\min}=140\cdot \frac{1}{7}=20.
Для пункта б) количество выпускников, которое не получило образование: N\,\theta_{\min}=140\cdot \frac{p_2}{s_2} =140\cdot \frac{1/5}{2}=140\cdot \frac{1}{10}=14.
Итого, на 6 тысяч выпускников больше получает образование.
Ответ: 6 тысяч.
в) ( 10 баллов) Теперь предположим, что государство решает не инвестировать в качество образования, а вместо этого делает обучение в менее престижном университете бесплатным (p_2=0). Будем считать, что каждый студент, получивший высшее образование, приносит положительную полезность государству, причем выпускники престижного университета увеличивают полезность государства на X, а выпускники менее престижного на 10. Найдите максимальное значение X, при котором государству выгоднее предоставлять бесплатно менее престижное образование, чем оставлять ситуацию, описанную в пункте a), если государство также не несёт никаких издержек на обучение студентов.
Из линии реакции, полученной в пункте a) :
p_1=\frac{1+p_2}{2}=\frac12
Пороговое значение \theta_{\min}, при котором студенты начинают поступать в менее престижный университет:
\theta_{\min}=\frac{p_2}{s_2}=\frac{0}{1}=0
Пороговое значение \hat{\theta}, при котором студенты начинают поступать в престижный университет:
\theta=\frac{p_1-p_2}{s_1-s_2}=\frac{\tfrac12-0}{2-1}=\frac12
Определим число студентов в университетах
N_1=140(1-\theta)=140\!\left(1-\frac12\right)=140\cdot\frac12=70
N_2=140(\theta-\theta_{\min})=140\!\left(\frac12-0\right)=140\cdot\frac12=70
Вычислим полезности государства в двух ситуациях.
Случай А (из пункта а) ):
U_A=140\!\left(\frac34-\frac17\right)\cdot 10\;+\;140\!\left(1-\frac37\right)X
Случай В (при p_2=0 ):
U_B\;(p_2=0)=140\cdot\frac12\cdot 10\;+\;140\!\left(1-\frac12\right)X
Государству выгоднее делать образование бесплатным, если: U_B\geq U_A
Подставляем выражения:
140 \times \frac{1}{2} \times 10 + 140 \left(1 - \frac{1}{2}\right) X \ge 140 \left(\frac{3}{4} - \frac{1}{7}\right) \times 10 + 140 \left(1 - \frac{3}{7}\right) X
Решая это неравенство, получаем: X\leq 30
Следовательно, максимальное значение X, при котором государству выгодно делать обучение в менее престижном университете бесплатным: X=30.
Ответ: X=30.
г) ( 10 баллов) Из пункта в) следует, что при некоторых X полезность государства выше в ситуации, когда оно не предоставляет бесплатное высшее образование и оставляет систему частного образования как в пункте а). Используя модель задачи, объясните, почему государство не всегда выигрывает от предоставления бесплатного образования.
Государство не всегда выигрывает от предоставления бесплатного высшего образования, так как это влияет на выбор выпускников между престижным и менее престижным университетами.
Когда обучение в менее престижном университете становится бесплатным, больше студентов выбирают именно этот вариант, а в случае платного образования они могли бы поступить в престижный университет. В результате уменьшается число выпускников с более престижным образованием, что негативно сказывается на полезности государства.
Таким образом, предоставление бесплатного образования не всегда приводит к оптимальному результату. Государству необходимо учитывать баланс между доступностью образования и его качеством, а также влияние на будущие экономические показатели.