Формирование цен на такси. Олимпиада Колокольникова 2 тур 2025 (8 класс)
Рассмотрим линейный город, являющийся отрезком длины 10. Жители равномерно распределены на этом отрезке (то есть на каждый километр расстояния приходится одинаковое и достаточно большое число жителей). На разных концах города располагаются автопарки фирмы «A-Такси» в точке 0 и фирмы «Бубер» в точке 10. Обе фирмы занимаются перевозками жителей города и назначают свою цену на любую поездку по формуле P_i=S_i+kl, где i — это или А, или Б (для «А-Такси» и «Бубер», соответственно), S_i — стоимость подачи такси, k — стоимость одного километра поездки, а l — длина маршрута с учетом дороги от автопарка до потребителя. Правительство города обязало фирмы устанавливать цену за километр поездки на уровне дополнительных издержек на один километр пути. По состоянию на 2025 год средняя цена топлива на 10 километров равна 60 рублей, а водители готовы проехать километр пути за 4 рубля.
а) ( 2 балла) Найдите коэффициент k, который был зафиксирован государством для обеих фирм.
В этой задаче вам необходимо определить, какие цены будут назначать обе фирмы на свои услуги такси в первый теплый весенний день, когда все жители города хотят посетить загородный парк в точке 20. Каждый из жителей хочет совершить ровно одну поездку из города в парк. При этом за такую поездку они готовы заплатить любую цену, но стараются заплатить как можно меньше. Общий спрос на поездки составляет Q=10. Например, на отрезке от 2 до 6 живет 40\% всех жителей, и они потребляют Q=4 поездки.
Стоимость километра поездки складывается из расходов на прибыль водителя и издержек на топливо. Тогда k=4+60/10=10.
Ответ: k=10.
б) ( 4 балла) При фиксированных S_А и S_Б найдите координату точки, в которой жителю, живущему в этой точке, безразлично в какой фирме заказывать такси до загородного парка. Считайте, что разница между ценами S_А и S_Б не превышает 100.
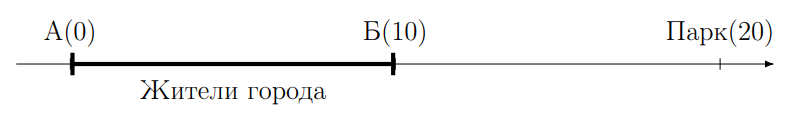
Найдем цены в обеих службах заказа такси для жителя, расположенного в точке x. Цена в «A-Такси» P_А равна сумме вызова такси и длины поездки, умноженной на 10. Длина поездки будет состоять из двух участков — от таксопарка А до клиента x (длина участка x-0=x ), и от клиента до загородного парка (длина участка 20-x ). В таком случае длина поездки «А-Такси» всегда будет равна 20, а значит P_А=S_А+10*20=S_А+200. Теперь найдем стоимость в сервисе «Бубер». Длина поездки будет состоять из двух участков —- от таксопарка Б до клиента x (длина участка — 10-x ), и от клиента до загородного парка (длина участка 20-x ).
Тогда общая длина маршрута равна l(x)=10-x+20-x=30-2x, тогда P_Б=S_Б+10*(30-2x)=S_Б+300-20x.
Найдем расположение безразличного клиента. Потребителю будет безразлично, в каком сервисе заказывать при равных ценах поездки в «А-Такси» и «Бубере»:
S_А + 200 = S_Б + 300 - 20x \\ 20x = S_Б - S_А + 100 \\ x = \dfrac{S_Б - S_А}{20} + 5
Ответ: Координата необходимой точки: \dfrac{S_Б - S_А}{20} + 5
в) ( 4 балла) Найдите равновесные S_А и S_Б, которые установят фирмы, если они выбирают стоимости подачи одновременно и независимо.
Так как цена в «А-Такси» фиксированная при данном S_А, а в «Бубере» уменьшается при отдалении клиента от таксопарка А, то все жители, находящиеся дальше безразличного потребителя от точки А, будут вызывать в «Бубере», а остальные — в первом сервисе.
То есть Q_А = x = \frac{S_Б - S_А}{20} + 5, а Q_Б = 10 - x = 10 - \left( \frac{S_Б - S_А}{20} + 5 \right) = 5 + \frac{S_А - S_Б}{20}.
Так как издержки каждой поездки равны kl, то прибыли с каждой поездки для фирм постоянна и равна S_i.
Фирмы выбирают S_А и S_Б одновременно, следовательно, воспринимают цены друг друга заданными.
Запишем прибыль «А-Такси»:
\Pi_А = S_А Q_А = S_А \left( \frac{S_Б - S_А}{20} + 5 \right) = -\frac{S_А^2}{20} + \left( \frac{S_Б}{20} + 5 \right) S_А,
то есть П_А(S_А) — парабола ветвями вниз, и, значит, принимает свое максимальное значение в вершине
S_А = -\frac{\left(\frac{S_Б}{20} + 5\right)}{2 \cdot \left(-\frac{1}{20}\right)} = \frac{S_Б}{2} + 50
Запишем прибыль «Бубера»:
\Pi_Б = S_Б Q_Б = S_Б \left( 5 + \frac{S_А - S_Б}{20} \right) = -\frac{S_Б^2}{20} + \left( \frac{S_А}{20} + 5 \right) S_Б
то есть П_Б(S_Б) — парабола ветвями вниз, и, значит, принимает свое максимальное значение в вершине
S_Б = -\frac{\left(\frac{S_А}{20} + 5\right)}{2 \cdot \left(-\frac{1}{20}\right)} = \frac{S_А}{2} + 50.
Равновесие должно удовлетворять обоим равенствам:
\begin{cases} S_А = \dfrac{S_Б}{2} + 50 \\ S_Б = \dfrac{S_А}{2} + 50 \end{cases}
откуда S_А=100, \ S_Б=100.
Ответ: S_А=100, \ S_Б=100.
г) ( 2 балла) Какие цены для жителей города будут назначать фирмы «АТакси» и «Бубер», и по каким ценам будут совершаться поездки?
А-Такси» будет назначать всем одну и ту же цену P_А=S_А+200=300, а «Бубер» P_Б=100+300-20x, и так как x\in[0; \ 10], то цены будут назначены от 200 до 400. При этом поездки будут совершаться по цене 300 в «А-Такси» и по цене от 200 до 300 у «Бубера».
Ответ: «А-Такси» будет назначать всем цену P_А=300, «Бубер» будет назначать цену P_Б в диапазоне от 200 до 400, но продавать будет только по ценам от 200 до 300.