До связи
Провайдер мобильной связи «Вышлайн» ведет свою деятельность на двух рынках: рынке минут разговоров и рынке гигабайт интернета. На обоих рынках «Вышлайн» является монополистом, а предельные издержки производства минут и гигабайт нулевые, равно как и постоянные издержки. На рынке минут и на рынке гигабайт спрос предъявляют две группы потребителей: группа A и группа B. Спрос группы A на рынке минут имеет вид Q_m^A=100-P_m, а на рынке гигабайт — Q_g^A=60-P_g/3, где P_m — цена минуты разговора, а P_g — цена гигабайта интернета. Спрос группы B на рынке минут имеет вид Q_m^B=60-P_m/3, а на рынке гигабайт: Q_g^B=100-P_g. Группы имеют одинаковый размер и внутри каждой группы потребители одинаковые. Известно, что компания «Вышлайн» не может различать группы потребителей на обоих рынках.
а) ( 5 баллов) Найдите цены, которые монополист установит на обоих рынках, и максимальную прибыль компании «Вышлайн».
Найдём суммарный спрос на каждом из рынков. Получим суммарный спрос на гигабайты
Q_g = \begin{cases} 60 - \dfrac{P_g}{3}, & P_g \in (100; 180], \\ 160 - \dfrac{4}{3}P_g, & P_g \in [0; 100]. \end{cases}
Симметрично ситуация обстоит на рынке минут. Запишем прибыль монополиста на рынке гигабайт
\Pi_g = \begin{cases} 60P_g - \dfrac{P_g^2}{3}, & P_g \in (100; 180], \\ 160P_g - \dfrac{4}{3}P_g^2, & P_g \in [0; 100]. \end{cases}
1) На участке P_g\in(100;180] функция прибыли является параболой с ветвями вниз и вершиной в точке P_g=90<100, то есть не попадает в рассматриваемый участок.
2) На участке P_g\in[0;100] функция прибыли также является параболой с ветвями вниз и вершиной в точке P_g=60. Попадает под условие, а так как функция прибыли не имеет разрыва, то при цене P_g=60 будет достигаться максимальная прибыль (см. рисунок 1).
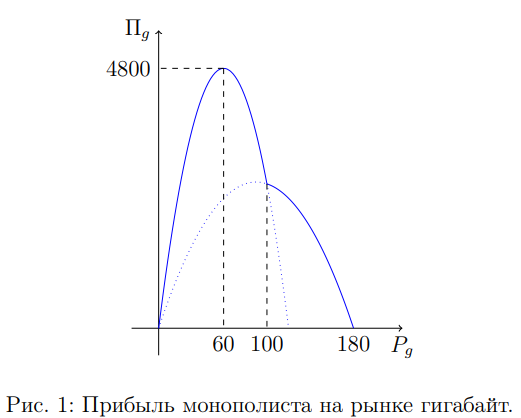
Аналогично для рынка минут. Таким образом, монополист установит одинаковые цены на обоих рынках P_g=P_m=60.
б) ( 20 баллов) Известно, что компания «Вышлайн» установила цены на уровне из пункта (а) и не может их изменить. Отдел аналитики компании предложил ввести кешбэк на продукцию для увеличения прибыли. Потребители могут выбрать для себя только одну категорию кешбэка: либо X\% кешбэк на минуты, либо Y\% кешбэк на гигабайты. Известно, что потребители воспринимают кешбэк как скидку и предпочитают ту альтернативу, при которой их излишек увеличится больше. Найдите оптимальные для компании «Вышлайн» ставки кешбэка X\% на минуты и Y\% на гигабайты. Увеличилась ли прибыль компании по сравнению со значением, которое вы определили в пункте а) ?
Цена зафиксирована на уровне P_g=P_m=60. Тогда «новая» цена для покупателя, выбравшего кешбэк на рынке минут, будет равна (1-x)P_m=(1-x)60, а «новая»
цена для выбравших кешбэк на рынке гигабайт будет равна (1-y)P_g=(1-y)60.
Рассмотрим три случая:
1.
a. Обе группы выбирают кешбэк на минуты;
b. Обе группы выбирают кешбэк на гигабайты;
2. Группа A выбирает гигабайты, группа B — минуты;
3. Группа A выбирает минуты, группа B — гигабайты.
Случай 1a и 1b.
Рассмотрим случай, когда обе группы будут выбирать кешбэк на минуты. Прибыль на рынке гигабайт не изменится по сравнению с пунктом a). Запишем прибыль монополиста на рынке минут в этом случае
\Pi_m = (1 - x) \cdot 60 \cdot \left( 160 - \frac{4 \cdot 60(1 - x)}{3} \right) = 60 \cdot \left( 160(1 - x) - \frac{4 \cdot 60(1 - x)^2}{3} \right).
Функция прибыли является параболой ветвями вниз относительно (1-x) и достигает своего максимума в вершине (1-x)=1, то есть оптимальная ставка кешбэка на минуты в этом случае x^*=0, значит кешбэк не будет введен. Аналогично для случая 1b.
Случай 2.
Запишем прибыль монополиста на рынке минут
\Pi_m = 40 \cdot 60 + (1 - x) \cdot 60 \cdot \left( 60 - \frac{60(1 - x)}{3} \right) = 40 \cdot 60 + 60 \cdot \left( 60(1 - x) - \frac{60(1 - x)^2}{3} \right)
Функция прибыли является параболой ветвями вниз относительно (1-x) и достигает своего максимума в вершине (1-x)=1, то есть оптимальная ставка кешбэка на минуты в этом случае x^*=0, значит кешбэк не будет введен. Аналогично на рынке гигабайт.
Случай 3 .
Рассмотрим изменение потребительских излишков при выборе группой A кешбэков на рынке минут (\Delta CS_m) и гигабайт (\Delta CS_g) на рисунке 2.
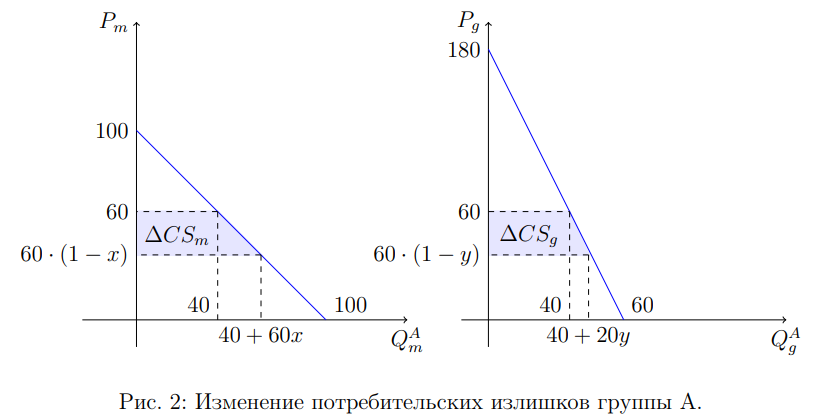
\Delta CS_m = \frac{100 - P_m + 100 - (1 - x)P_m}{2} \cdot P_m(1 - 1 + x) = \frac{80 + 60x}{2} \cdot 60x = (40 + 30x)60x
\Delta CS_g = \frac{60 - \frac{P_g}{3} + 60 - \frac{(1 - y)P_g}{3}}{2} \cdot 60y = \frac{80 + 2y}{2} \cdot 60y = (40 + 10y)60y
Для того, чтобы агент из группы A выбрал кешбэк на минуты, а не на гигабайты, должно выполняться (1) \quad \Delta CS_m > \Delta CS_g.
На данном этапе можно также заметить, что т.к. положения на рынках минут и гигабайт, а также спросы групп симметричны, следовательно, в оптимуме, x и y должны быть равны. Таким образом, соотношение 1 выполняется всегда. Группа A при равных x, \ y всегда будет выбирать кешбэк на минуты. Аналогично для группы B — она всегда будет выбирать кешбэк на гигабайты.
Запишем оптимизационную задачу монополиста на рынке минут.
\Pi_m = (1 - x) \cdot 60 \cdot (40 + 60x) + 40 \cdot 60 \rightarrow \max_{x \in [0,1]}.
Функция прибыли на рынке минут является параболой ветвями вниз, максимум которой достигается в вершине x^*=1/6. Аналогично для рынка гигабайт и y^*. Следовательно, оптимальные x^*, \ y^*=1/6. Сравним прибыли до введения кешбэка
\Pi_{(a)} = 60 \cdot 80 = 4800 и после \Pi_{(б)} = \frac{5}{6} \cdot 60 \cdot \left( 40 + 60 \cdot \frac{1}{6} \right) + 2400 = 4900 > 4800, то есть аналитики были правы, введение кешбэка увеличило прибыль