Максимизация йогуртов
Технология производства йогуртов, которые намеревается выпускать предприниматель Винокуров, описывается функцией Q = -\frac{L^3}{3} + 10L^2 + 150L, L<25, Q — количество йогуртов, L — количество единиц труда.
Труд работников, которых можно нанять на совершенно конкурентном рынке труда, молодой предприниматель намеревается оплачивать готовой продукцией, т. е. выдавая им йогурты.
Выяснилось, что работники меньше, чем за 234 йогурта, работать не согласны. Определите, сколько работников следует нанять предпринимателю Винокурову, желающему, естественно, получить максимальную прибыль.
Наняв L работников, Винокуров платит им 234L йогуртов, а получает взамен Q(L) йогуртов. Какова бы ни была цена, по которой он планирует продавать йогурты, ему выгодно максимизировать количество йогуртов, которые остаются у него после расчётов с работниками, то есть величину Q(L)-234L
Предположим, что оптимальное L>0. Тогда необходимое условие экстремума — равенство производной нулю. Решив уравнение -L^2+20L+150-234=0 относительно L, получим L=6 или L=14. Но при этих значениях L Q(6)=198<Q(14)=224, (6)<w=234, т.е. прибыль отрицательна. При L=0 получаем нулевую прибыль. Это и есть оптимум.
На рисунке изображен график Q(L)-234L.
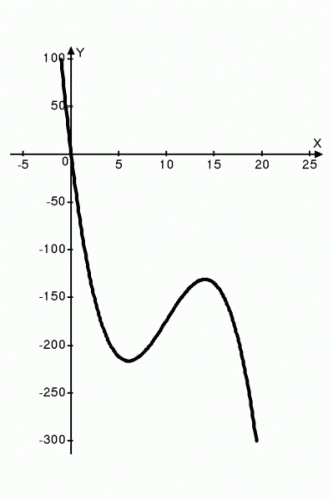
Ответ:
При такой технологии производства и цене труда предприниматель не получит положительной прибыли, нанимать работников и организовывать производство йогуртов не следует, т. е. L*=0.