Задача 1.1.2
Лобов N. А. производит кольца власти (x) и единицы IT (y), используя сканеры (s) и рыб-вуалехвостов из аквариума учебного центра Вороново (f). Производственные функции колец власти и IT имеют вид соответственно
x = \min\left\{ \frac{s^2}{4}, f^2 \right\}, \quad y = \min\left\{ s^2, \frac{f^2}{4} \right\}
Лобов имеет в своем распоряжении всего 2 сканера и 2 вуалехвоста. На рынке одну единицу IT меняют на два кольца власти.
а) Изобразите КПВ Лобова N. А. на графике в координатах колец власти и единиц IT. Запишите КПВ аналитически.
\\\\
Летний олимпиадный лицей, 2023
Индексами x, \ y будем обозначать объёмы ресурсов, используемых в производстве соответственно x и y. Так как для производства каждого из товаров нужны оба ресурса, КПВ получается совмещением двух ограничений:
\begin{cases} 4x = s_x^2 \\ y = s_y^2 \\ s_x + s_y \leq 2 \end{cases} \quad \begin{cases} x = f_x^2 \\ 4y = f_y^2 \\ f_x + f_y \leq 2 \end{cases} \Rightarrow \begin{cases} 2\sqrt{x} + \sqrt{y} \leq 2 \\ \sqrt{x} + 2\sqrt{y} \leq 2 \end{cases}
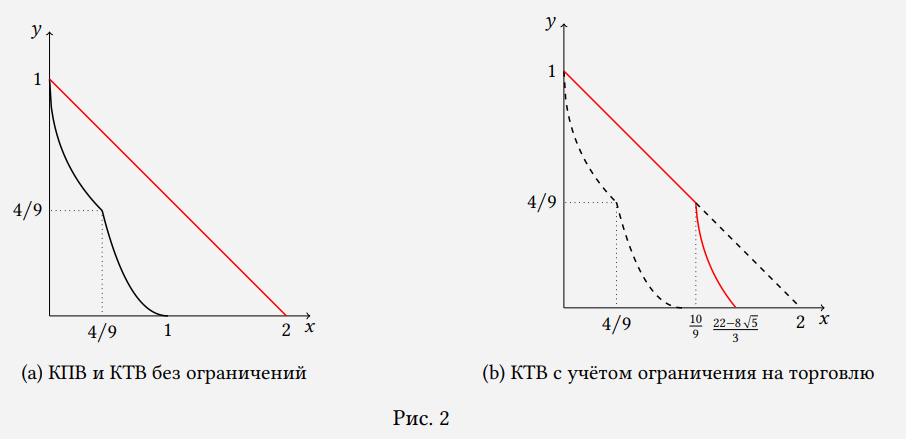
КПВ получаем как нижнюю огибающую этих ограничений: рис. 2a. Оба они выпуклы, их границы соединяют точки, соответственно (0, \ 4), \ (1, \ 0) и ( 0, \ 1), \ (4, \ 0) , поэтому пересекутся в некоторой точке. Для нахождения точки пересечения решим систему
\begin{cases} 2\sqrt{x} + \sqrt{y} = 2 \\ \sqrt{x} + 2\sqrt{y} = 2 \end{cases}
Получаем точку (4/9, \ 4/9). Для аналитического выражения лишь добавим ограничения в систему, явно выражать y или x не требуется:
\begin{cases} 2\sqrt{x} + \sqrt{y} = 2, & x \in \left[\frac{4}{9}, 1\right] \text{ и } y \in \left[0, \frac{4}{9}\right] \\ \sqrt{x} + 2\sqrt{y} = 2, & x \in \left[0, \frac{4}{9}\right) \text{ и } y \in \left(\frac{4}{9}, 1\right] \end{cases}
б) Изобразите КТВ Лобова N. А. на графике предыдущего пункта.
КТВ — прямая с наклоном 0,5, поскольку 1 единицу y обменивают на 2 единицы x. Наиболее высоко лежащая прямая, имеющая хотя бы одну точку пересечения с КПВ проходит через точку (0, \ 1) : y=1-0,5x, красная линия на рис. 2a.
в) Предводительница Алёна С. была озадачена результатом торговли, из-за чего запретила Лобову N. А. продавать кому-либо более 5/9 единиц IT. Учитывая новые ограничения, изобразите КТВ Лобова на графике и запишите аналитическую зависимость.
Можно продавать любое количество y не более 5/9, поэтому доступны любые точки КТВ, лежащие выше прямой y=4/9. Для нахождения оставшегося участка КТВ необходимо сдвинуть всю КПВ по направлению, соответствующему продаже ровно 5/9 единиц y. То есть необходимо сдвинуть КПВ на 5/9 единиц вниз и на 2*5/9=10/9 единиц вправо. После сдвига нижний участок КПВ таким образом окажется под осью x, так что КТВ будет состоять только из двух участков: красная кривая на рис. 2b.
Аналитическая зависимость:\begin{cases} y + 0.5x = 1, & x \in [0, \frac{10}{9}] \text{ и } y \in [\frac{4}{9}, 1] \\ \sqrt{x - \frac{10}{9}} + 2\sqrt{y + \frac{5}{9}} = 2, & x \in \left(\frac{10}{9}, \frac{22 - 8\sqrt{5}}{3}\right] \text{ и } y \in [0, \frac{4}{9}) \end{cases}