Экономико-геометрический этюд: рентабельность монополиста
Спрос на продукцию монополиста линеен, а средние издержки ее производства постоянны. Известно, что при оптимальном для монополиста объеме выпуска соответствующий объем выручки составляет 8/9 от максимально возможного. Какова рентабельность фирмы в точке оптимума?
Геометрическое решение:
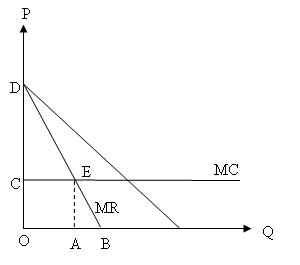
Значение выручки в некой точке q равно площади под графиком предельной выручки на отрезке [0;q]. Поэтому
\frac{TR(Q^*)}{TR_{\text{max}}} = \frac{S_{ODEA}}{S_{ODB}} = 1 - \frac{S_{AEB}}{S_{ODB}}.
Треугольники AEB и ODB подобны, поэтому \frac{S_{AEB}}{S_{ODB}} = \frac{AE^2}{OD^2}. Значит,
\frac{TR(Q^*)}{TR_{\text{max}}} = 1 - \frac{AE^2}{OD^2} = \frac{8}{9} \Rightarrow \frac{OC}{OD} = \frac{1}{3} \Rightarrow \frac{OC}{CD} = \frac{1}{2} \Rightarrow S_{DCE} = S_{OCEA} \Rightarrow \pi = TC.
Проверим себя аналитически:
P = a - bQ; \quad MR = a - 2bQ = MC = c = \text{const} = AC
Q^* = \frac{a-c}{2b}, \quad P^* = \frac{a+c}{2}.
TR = P(Q) \cdot Q = (a - bQ) \cdot Q \rightarrow \max \Rightarrow Q = \frac{a}{2b}, \quad TR_{\text{max}} = \frac{a^2}{4b}.
По условию, TR(Q*)=\frac{8}{9} TR_{max}
\frac{a^2 - c^2}{4b} = \frac{8}{9} \cdot \frac{a^2}{4b} \Rightarrow a = 3c.
\frac{\pi(Q^*)}{TC(Q^*)} = \frac{TR(Q^*)}{TC(Q^*)} - 1 = \frac{(a^2 - c^2)/4b}{c \cdot (a-c)/2b} - 1 = \frac{(3c)^2 - c^2}{2c(3c-c)} - 1 = 2 - 1 = 1.
Ответ:
100%