Неравенство среднедушевых доходов
Некое общество состоит из двух социальных групп, внутри каждой из которых доход распределен равномерно. Известно, что среднедушевой доход в первой группе составляет 5 тыс. руб. в месяц, во второй – 25 тыс. руб. в месяц, а во всем обществе среднедушевой доход составляет 20 тыс. руб. в месяц. Определите значение коэффициента Джини для этого общества.
Обозначим количество членов более бедной социальной группы за N_1, более богатой - за N_2, а доходы групп соответственно за I_1 и I_2. Тогда:
\frac{I_2 + I_1}{N_2 + N_1} = 20; \quad \frac{I_1}{N_1} = 5; \quad \frac{I_2}{N_2} = 25
I_1 = 5N_1; \quad I_2 = 25N_2; \quad \frac{25N_2 + 5N_1}{N_2 + N_1} = 20
25N_2 + 5N_1 = 20N_2 + 20N_1; \quad N_2 = 3N_1
\frac{N_1}{N_2 + N_1} = 0,25; \quad \frac{I_1}{I_2 + I_1} = \frac{5N_1}{75N_1 + 5N_1} = 0,0625
Кривая Лоренца будет иметь следующий вид:
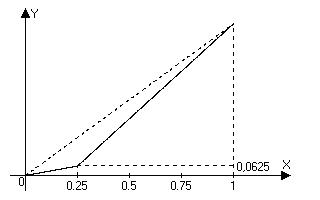
Построив ее, легко посчитать коэффициент Джини:
G = \frac{0{,}5 - 0{,}5 \cdot 0{,}25 \cdot 0{,}0625 - 0{,}5 \cdot (1 + 0{,}0625) \cdot 0{,}75}{0{,}5} = 0{,}1875
Ответ:
0,1875.