Эластичность на линейном спросе
На конкурентом рынке труда работают два типа фирм, каждый с линейной кривой спроса на труд. Интересно, что максимальная зарплата, которую готовы платить фирмы обоих типов (та самая <<цена выключения>> спроса), одинакова. Однако фирмы второго типа всегда проявляют большую активность: при любой ставке заработной платы w типичная фирма второго типа нанимает в \alpha>1 раз больше работников, чем фирма первого типа.
Экономисты, изучавшие этот рынок, обнаружили любопытный факт: существует такой объём суммарной занятости L, при котором чувствительность спроса первой группы фирм к изменению зарплаты (эластичность спроса по заработной плате) оказывается ровно в три раза ниже, чем эластичность общего рыночного спроса. Более того, при этом же уровне занятости L зарплата, которую готов платить рынок, оказывается на четверть выше, чем у фирм первой группы.
Определите, во сколько раз именно фирмы второго типа активнее нанимают работников по сравнению с первыми.
Построим график и отметим необходимые для решения точки A, \ B, \ C, \ D, \ E, а также соотношения величины найма при единой заработной плате w=w_C.
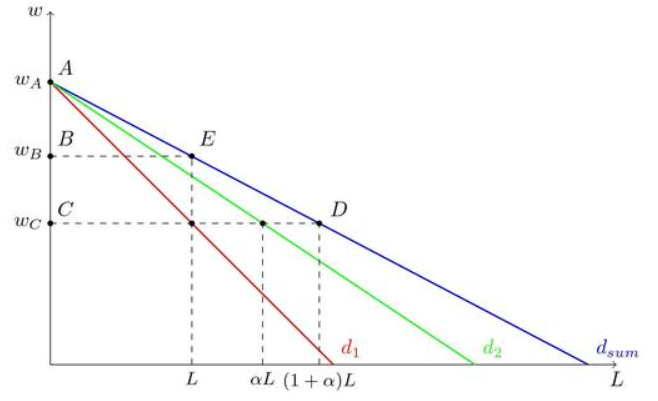
Заметим, что эластичность первой кривой спроса при цене w_C=w_1^s(L) равна:
E_1 = \frac{w_C}{w_A - w_C}
Аналогично из геометрического смысла эластичности эластичность суммарного спроса при цене w_B = w_{\text{sum}}^s(L) равна:
E_{\text{sum}} = \frac{w_B}{w_A - w_B}
Так как по условию E_{\text{sum}} = 3E_1 имеет следующее соотношение:
\frac{w_B}{w_A - w_B} = 3 \cdot \frac{w_C}{w_A - w_C} \implies \frac{w_A - w_C}{w_A - w_B} = 3 \cdot \frac{w_C}{w_B} \quad (1)
Кроме того, заметим, что треугольники ABE и ACD подобны (по двум углам), а значит можно записать соотношения сходственных сторон:
\frac{BE}{CD} = \frac{AB}{AC} \quad \text{или} \quad \frac{L}{(1 + \alpha)L} = \frac{w_A - w_B}{w_A - w_C} \Rightarrow \frac{1}{1 + \alpha} = \frac{w_A - w_B}{w_A - w_C} \implies \frac{w_A - w_C}{w_A - w_B} = 1 + \alpha \quad (2)
Используя равенства (1) и (2), получаем:
\frac{w_C}{w_B} = 1 + \alpha
Из условия <<при этом же уровне занятости L зарплата, которую готов платить рынок, оказывается на четверть выше, чем у фирм первой группы>> получаем соотношение
w_B = 1.25w_C \Rightarrow \frac{w_C}{w_B} = \frac{4}{5} \Rightarrow 3 \cdot \frac{4}{5} = 1 + \alpha \Rightarrow \alpha = 1.4
А значит более активные фирмы нанимают на 40\% больше работников.
Ответ:
40\%