Сложение кривых Лоренца
В двух странах с одинаковым ВВП на душу населения коэффициенты Джини отличаются на единицу. Государство с менее равномерным распределением доходов – тоталитарное и милитаризованное – решило развязать войну со своим более демократичным соседом. Однако, несмотря на значительные расходы (на кампанию было потрачено около 75% ВВП), агрессор потерпел явную неудачу. В ходе кровопролитных боев погибло 60% населения нападающей страны. Для сравнения, демократическое государство потратило на оборону только 25% ВВП, пожертвовав жизнями 20% населения. В итоге страны решили заключить мирный договор и образовать союзное государство. Оказалось, что коэффициент Джини в объединенном государстве равен 0,5. Каков был бы коэффициент Джини, если бы страны решили объединиться до войны?
Коэффициенты Джини отличаются на 1 \Rightarrow один из них равен 0 (в демократической стране), а другой – 1 (в тоталитарной).
Обозначим демократическую страну «D», а тоталитарную – «T», Y – ВВП, P – численность населения, момент до войны – «0», момент после войны – «1».
Тогда
Y_1^D = 0{,}75 Y_0^D, \quad P_1^D = 0{,}8 P_0^D.
Y_1^T = 0{,}25 Y_0^T, \quad P_1^T = 0{,}4 P_0^T.
Отсюда
\frac{Y_1^D}{Y_1^T} = 3 \frac{Y_0^D}{Y_0^T} \cdot \frac{P_1^D}{P_1^T} = 2 \frac{P_0^D}{P_0^T}.
Но в силу равенства ВВП на душу населения до войны \frac{Y_0^D}{P_0^D} = \frac{Y_0^T}{P_0^T} \Rightarrow \frac{Y_0^D}{Y_0^T} = \frac{P_0^D}{P_0^T}.
Значит,\frac{Y_1^D}{Y_1^T} = 3 \frac{Y_0^D}{Y_0^T} = 3 \frac{P_0^D}{P_0^T} = 1{,}5 \frac{P_1^D}{P_1^T}..
Обозначим \frac{Y_1^T}{Y_1^T} = x, \quad \frac{P_1^D}{P_1^T} = y. Тогда \frac{Y_1^T}{Y_1^T} = x, \quad \frac{P_1^D}{P_1^T} = y.
Поймем, как будет выглядеть кривая Лоренца объединенного государства. Самые бедные в новом государстве – это жители бывшего тоталитарного государства, имеющие нулевые доходы. Их доля в населении нового государства равна \frac{P_1^T}{P_1^T + P_1^D} = \frac{1}{y+1}, поэтому на отрезке [0; \frac{1}{y+1}] кривая Лоренца нового государства будет совпадать с осью абсцисс. «Средний класс» в новом государстве будут составлять бывшие жители демократическо
го государства. Вместе с бедными они будут составлять почти все население нового государства, а суммарная доля доходов этих групп населения в общем ВВП равна (0 + \frac{Y_1^T}{Y_1^T + Y_1^D} = \frac{x}{x+1}. Кроме того, внутри среднего класса распределение доходов абсолютно равномерно, поэтому следующий участок общей кривой Лоренца будет отрезком прямой с концами в точкахA\left(\frac{1}{y+1}; 0\right) и B\left(1; \frac{x}{x+1}\right) . И, наконец, соединяя точку B с точкой C(1;1), получаем отрезок общей кривой Лоренца, «ответственный» за богатых, то есть за ту самую крайне малочисленную группу населения тоталитарной страны, располагавшую всем ее ВВП. В итоге общая кривая Лоренца имеет вид:
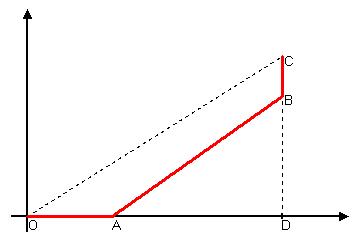
Тогда коэффициент Джини равен \frac{S_{OABC}}{S_{OCD}} = 1 - \frac{S_{ABD}}{S_{OCD}} = 1 - \frac{x}{x+1} \cdot \frac{y}{y+1} = \frac{1}{2}.
Учитывая то, что x=1,5y, имеем:
\frac{1{,}5y^2}{(1{,}5y+1)(y+1)} = \frac{1}{2}
3y^2 - 5y - 2 = 0 \Rightarrow y = 2 = \frac{P_1^D}{P_1^T}
Значит, \frac{Y_1^D}{Y_0^T} = \frac{P_0^D}{P_0^T} = \frac{2}{2} = 1.
Получается, что до войны страны имели одинаковый ВВП и одинаковую численность населения!
Если бы страны объединились до войны, то общая кривая Лоренца имела бы качественно такой же вид, как и в случае объединения после войны. Следуя описанной выше логике построения этой кривой, нетрудно установить, что совокупная кривая Лоренца до войны проходила бы через точки (0; 0), (0; 0{,}5), (1; 0{,}5), (1; 1), и совокупный коэффициент Джини был бы равен 0,75.
Ответ:
0,75