Спрос рождает предложение
Фирма «Мориарти» является монополистом на региональном рынке свежих слив. Функция спроса на сливы в регионе имеет вид q_d(p)=180-p_d (при ценах выше 180 потребители ничего не покупают), где p_d — цена на региональном рынке. Фирма владеет одним заводом, издержки производства слив на котором зависят от объема выпуска следующим образом:
TC_1(q_1) = \begin{cases} q_1^2 + 12q_1 + 2017, & \text{если} \ q > 0; \\ 0, & \text{если} \ q = 0. \end{cases}
У фирмы есть возможность открыть второй завод, функция издержек на котором будет такой же, как на первом (объем выпуска на втором заводе обозначим за q_2 ).
а) (10 баллов) Является ли открытие второго завода оптимальным решением с точки зрения максимизации прибыли?
б) (20 баллов) Фирма «Мориарти» рассматривает возможность выхода на рынок соседнего региона. Если она это сделает, то останется монополистом в своем регионе, а в соседнем сможет продать любой объем выпуска q_f по цене 120.Стоит ли фирме выходить на новый для нее рынок? Если да, то стоит ли при этом открывать второй завод?
Сначала найдем общую функцию издержек для случая открытия второго завода, то есть при Q=q_1+q_2, q2>0. При оптимальном распределении выпуска между заводами (если на обоих заводах производится ненулевое количество товара) предельные издержки на двух заводах должны быть равны. Если это будет не так, то достаточно переместить небольшой объем производства с того завода, где издержки производства последней единицы больше, туда, где они меньше, и издержки уменьшатся при неизменной выручке.
Значит, должно быть выполнено
MC_1(q_2) = MC_2(q_2), \\ 2q_1 + 12 = 2q_2 + 12, \\ q_1 = q_2 = \frac{Q}{2}.
Составим функцию общих издержек от суммарного объема выпуска:
TC(Q) = TC_1(q_1) + TC_2(q_2) = 2 \cdot \left( \left(\frac{Q}{2}\right)^2 + 12\left(\frac{Q}{2}\right) + 2017 \right) = \frac{Q^2}{2} + 12Q + 4034.
Таким образом, в обоих пунктах задачи фирма может выбирать между функцией издержек, которая дана в условии, и функцией издержек (1.1).
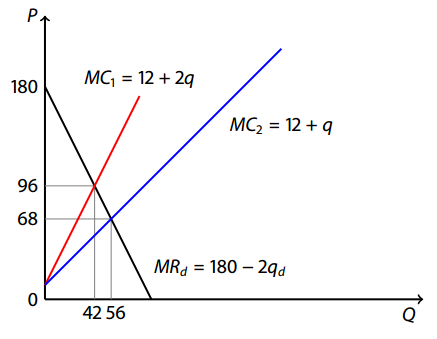
а) В случае использования фирмой только одного завода (q_1=Q>0 ) функция прибыли имеет вид
\pi(Q) = (180 - Q)Q - Q^2 - 12Q - 2017
Это парабола с ветвями вниз и вершиной в точке Q^*=42. Максимальная прибыль при этом равна 1511.
В случае использования фирмой двух заводов (q_1=q_2=Q/2>0 ) функция прибыли имеет вид
\pi(Q) = (180 - Q)Q - \frac{Q^2}{2} - 12Q - 4034.
Это парабола с ветвями вниз и вершиной в точке Q^{**}=56. Максимальная прибыль при этом равна 670.
Максимальная прибыль с одним заводом больше, поэтому второй открывать не нужно.
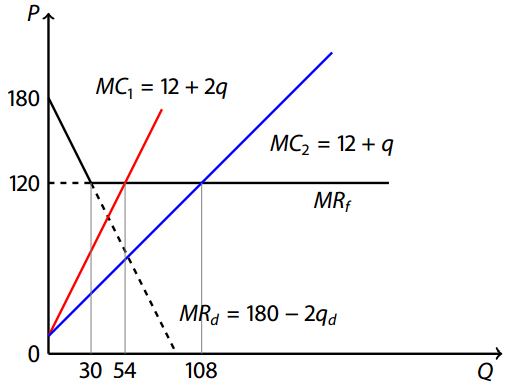
б) С появлением второго рынка фирме нужно решить две задачи:
1) Как распределять произведенный выпуск между рынками?
2) Сколько всего производить?
Ответ на первый вопрос получается при приравнивании предельной выручки на двух рынках. Действительно, каждую единицу товара нужно продавать там, где она сильнее увеличивает выручку. Предельная выручка на внутреннем рынке MR_d(q_d)=180−2q_d убывает и при малых значениях q_d больше 120 (предельной выручки на внешнем рынке). Значит, продавать товар на внутреннем рынке нужно до тех пор, пока не будет выполнено 180−2q_d=120, а затем нужно переключиться на внешний, так как выручка на внутреннем будет больше. Отсюда получаем q^*_d=q^{**}_d=30, а оптимальная цена внутреннего рынка равна 150 (этот результат не зависит от того будет ли фирма выходить на внешний рынок, осуществляя производство продукции только на одном или одновременно на двух заводах). Итак, фирма получит на внутреннем рынке выручку, равную 4500.
Ответить на второй вопрос можно, приравняв предельную выручку, равную цене внешнего рынка, к общим предельным издержкам. Поскольку предельные издержки (как в случае одного, так и в случае двух заводов) возрастают, нужно продавать товар, пока предельный доход их превышает, то есть пока прибыль увеличивается. Получаем:

Прибыль в случае одного завода меньше, чем прибыль в случае двух заводов (1799<2698).
Значит, открывать второй завод выгодно. При этом максимальная прибыль больше той, что была в пункте а), так что выход на второй рынок был оправдан.