Издержки миграции
В стране, состоящей из двух регионов E и W, производится при использовании труда два товара: сыр пармезан (X) и персики (Y). В регионе E единица труда может изготовить 2 единицы пармезана или 2 единицы персиков. В регионе W единица труда может изготовить 4 единицы пармезана или 1 единицу персиков. В каждом регионе есть 15 единиц труда. Регионы не обмениваются технологиями.
1. Постройте кривую производственных возможностей (КПВ) страны, если тру- довые ресурсы абсолютно мобильны (возможно перемещение любого числа единиц труда из одного региона в другой без издержек). Подпишите ее КПВ1*.*
2. Постройте на том же графике КПВ страны, если трудовые ресурсы абсолютно не мобильны (перемещение единиц труда между регионами невозможно). Подпишите ее КПВ2*.*
3. Предположим теперь, что миграция m единиц труда из одного региона в другой требует дополнительных затрат труда в размере , причём эти единиц оплачиваются регионом, из которого уезжают трудовые ресурсы. Постройте на том же графике КПВ страны и подпишите ее КПВ3*.*
4. Сравните полученные в предыдущих пунктах производственные множества: верно ли, что одно из них содержит все остальные? Верно ли, что одно из них содержится во всех остальных? Приведите содержательное экономическое объяснение получившихся ответов.
Ответ
1) (5 баллов) Если ресурсы абсолютно мобильны, то весь труд будет работать только по лучшим технологиям. Поэтому все иксы будут производиться в E, а все игреки — в W:
(a) 3 балла за указание на распределение всего труда по лучшим технологиям
(b) 2 балла за верный ответ (при наличии первого пункта)
2) (5 баллов) Если ресурсы абсолютно не мобильны, то перед нами стандартная задача сложения двух линейных КПВ:
КПВ региона W переместится вверх на 30, а КПВ региона E переместится вправо на 60. Первый участок:
Второй участок:
Таким образом, искомая КПВ имеет вид:
(a) 3 балла за сложение КПВ
(b) 2 балла за верный ответ
3) (10 баллов) Предположим, что мы из региона E перебросили в регион W m единиц труда. Тогда КПВ регионов имеют вид:
Общая КПВ имеет вид:
Заметим, что при фиксированном x первая строчка убывает по m, а вторая возрастает по m. Значит, для фиксированного x выгодно значение m>0, при котором x лежит на границе этих двух частей, т.е. 60+4m=x.
Значит,
или
Проделаем аналогичные рассуждения, если ресурсы перекидываются из области W в область E.
Предположим, что мы из региона W перебросили в регион E m единиц труда.
Тогда КПВ регионов имеют вид:
Общая КПВ имеет вид:
Заметим, что при фиксированном x первая строчка возрастает по m, а вторая убывает по m. Значит, для фиксированного x выгодно значение m>0, при котором x лежит на границе этих двух частей, т.е. 60−5m=x(1)
Значит,
или
Теперь заметим, что при выгоден второй случай (перекидывание ресурсов из W в E), а при x>60 — первый (перекидывание ресурсов из E в W). Значит, итоговая КПВ имеет вид
(a) по 2 балла за вывод КПВ при переброске m единиц (из W в E, из E в W)
(b) по 2 балла за упрощение КПВ (избавление от m) в каждом из двух случаев
(c) 2 балла за объединение систем и ответ
Все КПВ изображены на рисунке ниже.
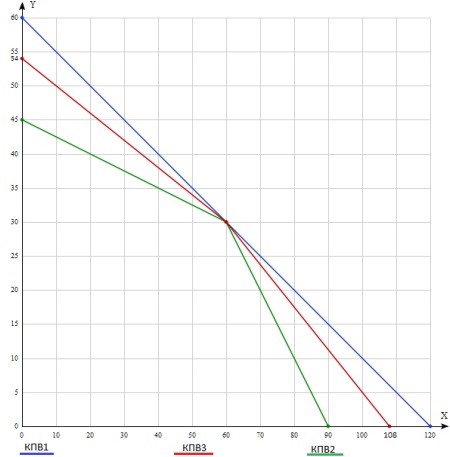
4) (5 баллов) Действительно (см. рис. и аналитические уравнения КПВ), при абсолютной мобильности ресурсов могут быть получены все точки производственного множества случаев с ограниченной мобильностью ресурсов и без мобильности. Действительно, все точки производственного множества случая немобильных ресурсов могут быть реализованы при частично мобильных и абсолютно мобильных ресурсах. За этими результатами стоит следующая экономическая интуиция. Во-первых, при наличии издержек миграции потерянная часть рабочей силы могла бы при отсутствии издержек использоваться для производства дополнительных товаров. Поэтому наличие издержек миграции ухудшает положение. Во-вторых, наличие возможности миграции, пусть и с издержками, не ухудшает положение по сравнению с отсутствием такой возможности.
(a) 3 балла за верный и обоснованный ответ на один из вопросов
(b) 5 баллов за верный и обоснованный ответ на оба вопроса (эти баллы не суммируются)
Примечание:
За общие рассуждения (о полезности миграции и т.д.), которые не показывали возможность реализации всех вариантов одной КПВ при другой КПВ, баллы не ставились