КПВ и миграция
В стране 1 могут производиться два товара –– X и Y. Есть две технологии производства товара X –– старая и новая. При производстве по старой технологии одна единица труда производит одну единицу товара X. При производстве по новой технологии одна единица труда производит две единицы товара X, однако произвести по новой технологии можно не более 200 единиц товара X, так как количество станков, нужных для производства по этой технологии, в стране ограничено. Для товара Y ситуация абсолютно такая же: есть такие же технологии с таким же ограничением для новой технологии. В стране 1 есть 150 единиц труда. Страна 2 ничем не отличается от страны 1, кроме того, что в ней есть не 150, а только 50 единиц труда.
В пунктах а)–в) укажите на графиках координаты крайних точек и точек излома КПВ.
а) ( 6 баллов) Постройте КПВ страны 1 и КПВ страны 2.
Начнем со Страны 1. Если произвести 200 единиц товара Y по новой технологии, на это уйдет 200/2=100 единиц труда, оставшиеся 150-100=50 единиц труда произведут 50 единиц товара Y по старой технологии. Значит максимальное количество товара Y, которое можно произвести в стране 1, равно 250. Получаем крайнюю точку (0, \ 250).
Теперь начнем производить товар X. Чтобы произвести единицу X c минимальными альтернативным издержками, нужно начать производить товар X по новой технологии, а уменьшать производство товара Y по старой, менее эффективной технологии. Альтернативные издержки будут равны 1/2. Так будет продолжаться до тех пор, пока либо не будет закрыто все производство Y по старой технологии, либо не мы не столкнемся с ограничением X\leq 200 по новой технологии. Первое настанет раньше, так как всего 50 единиц Y производились по старой технологии, и когда они будут исчерпаны, мы произведем 50/(1/2)=100 единиц X, что меньше 200. Получаем ключевую точку (100, \ 250-50)=(100, \ 200).
После прохождения этой ключевой точки, производя X, мы будем отказываться от производства Y по новой технологии, и альтернативные издержки будут равны 1. Это будет продолжаться до достижения ограничения X\leq 200. Для увеличения X co 100 до 200, придется отказаться от 100 единиц Y. Получаем ключевую точку (200, \ 200-100)=(200, \ 100).
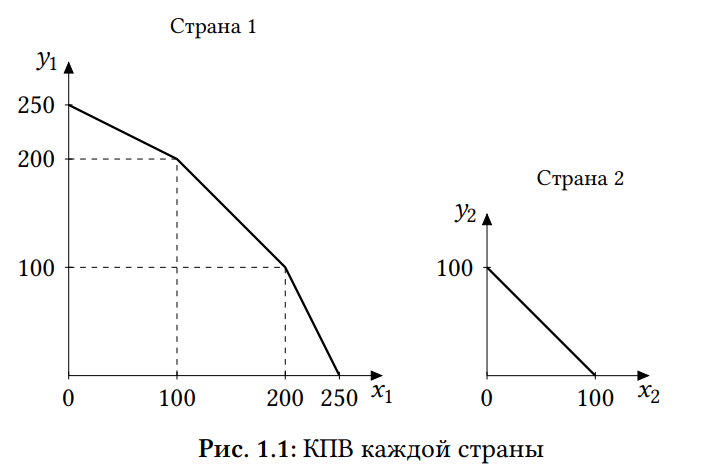
На последнем участке нам придется производить X по старой технологии, и отказываться от производства Y по новой технологии. Альтернативные издержки равны 2. Всего так можно произвести 50 единиц X, получаем последнюю точку (250, \ 0).
Ее также можно получить, пользуясь соображениями симметрии.
Страна 2:
Поскольку в стране 2 всего 50 единиц труда, которые по новой технологии могут произвести 100<200 единиц любого товара, в стране товары будут производиться только по новой технологии. Поэтому альтернативные издержки всегда равны 1. КПВ есть линейная функция Y=100-X.
Обе КПВ изображены на Рис. 1.1
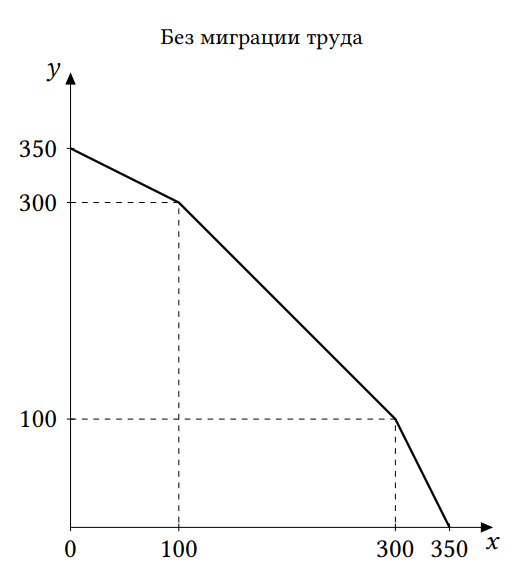
б) ( 6 баллов) Постройте общую КПВ двух стран, если миграция труда между странами невозможна.
Сложить две КПВ можно стандартным образом. Заметим, что альтернативная стоимость производства каждого товара в Стране 2 постоянна и равна 1 единице другого товара –– так же, как на среднем участке КПВ Страны 1. Следовательно, при добавлении КПВ Страны 2 к КПВ Страны 1 у последней как бы «удлинится» этот участок –– две страны вместе смогут произвести на нем 200 единиц любого из товаров с альтернативной стоимостью 1.
в) ( 5 баллов) Постройте общую КПВ двух стран, если возможна свободная миграция труда между странами.
В стране 2 из-за небольшого населения возможности производства по новой технологии недоиспользуются, и мы можем это исправить, направив в страну 2 труд из страны 1. По сути дела мы получаем одну большую страну, в которой 150+50=200 единиц труда, причем по новой технологии можно произвести не более 200+200=400 единиц каждого товара. 200 единиц труда как раз и могут произвести максимально 400 единиц, так что весь труд можно задействовать в производстве по новой технологии. Альтернативные издержки равны 1, и общая КПВ есть линейная функция Y=400-X.
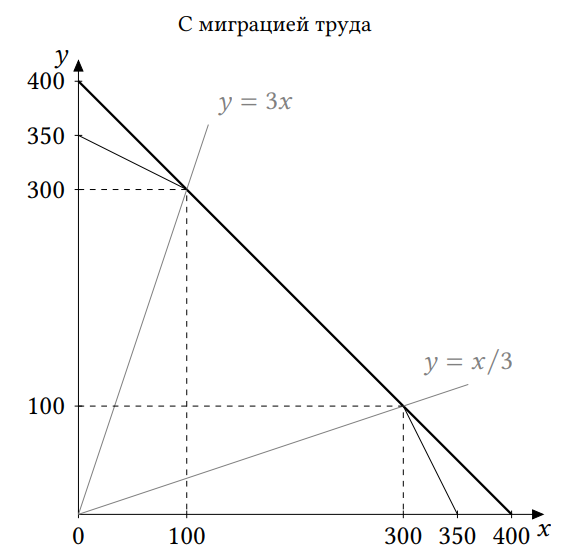
г) ( 3 балла) Если товары X и Y потребляются только в пропорции k единиц товара Y на 1 единицу товара X, то при каких значениях k>0 суммарное потребление товаров в странах увеличится в пункте в) по сравнению с пунктом б)?
КПВ из пункта в) совпадает с КПВ из пункта б) на среднем участке и лежит выше нее на крайних участках. Потребление увеличится, если объемы производства лежат на крайних участках КПВ. Решая графически, получаем k<1/3 или k>3, то есть k \in \left(0; \tfrac{1}{3}\right) \cup \left(3; +\infty\right).